题目内容
8.已知tanα=2,求下列各式的值(Ⅰ)$\frac{4sinα-2cosα}{5cosα+3sinα}$
(Ⅱ)$\frac{1}{4}{sin^2}α+\frac{1}{3}sinαcosα+\frac{1}{2}{cos^2}α+1$.
分析 由条件利用同角三角函数的基本关系,求得所给式子的值.
解答 解:∵已知tanα=2,(Ⅰ)∴$\frac{4sinα-2cosα}{5cosα+3sinα}$=$\frac{4tanα-2}{5+3tanα}$=$\frac{8-2}{5+6}$=$\frac{6}{11}$.
(Ⅱ)$\frac{1}{4}{sin^2}α+\frac{1}{3}sinαcosα+\frac{1}{2}{cos^2}α+1$=$\frac{\frac{1}{4}{•sin}^{2}α+\frac{1}{3}sinαcosα+\frac{1}{2}{•cos}^{2}α}{{sin}^{2}α{+cos}^{2}α}$+1
=$\frac{\frac{1}{4}{•tan}^{2}α+\frac{1}{3}tanα+\frac{1}{2}}{{tan}^{2}α+1}$+1=$\frac{1+\frac{2}{3}+\frac{1}{2}}{4+1}$+1=$\frac{43}{30}$.
点评 本题主要考查同角三角函数的基本关系的应用,属于基础题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
19.已知角α终边经过点 P(-5,-12),则 tanα 的值是( )
| A. | $\frac{12}{5}$ | B. | -$\frac{12}{5}$ | C. | $\frac{5}{12}$ | D. | -$\frac{5}{12}$ |
3.已知函数y=loga(x+c)(a>0且a≠1,a,c为常数)的图象如图,则下列结论正确的是( )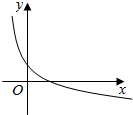

| A. | a>0,c>1 | B. | a>1,0<c<1 | C. | 0<a<1,0<c<1 | D. | 0<a<1,c>1 |
20.实数a>1,b>1是a+b>2的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.已知不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+2y-4≤0}\end{array}\right.$表示的平面区域恰好被面积最小的圆C:(x-a)2+(y-b)2=r2及其内部所覆盖,则圆C的方程为( )
| A. | (x-1)2+(y-2)2=5 | B. | (x-2)2+(y-1)2=8 | C. | (x-4)2+(y-1)2=6 | D. | (x-2)2+(y-1)2=5 |
18.下列函数中,在区间(1,+∞)上为增函数的是( )
| A. | y=-3x+1 | B. | y=$\frac{2}{x}$ | C. | y=x2-4x+5 | D. | y=|x-1|+2 |
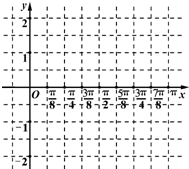 已知向量$\overrightarrow{a}$=($\sqrt{2}$sinx,$\frac{{\sqrt{2}}}{2}$(cosx+sinx)),$\overrightarrow{b}$=(2cosx,sinx-cosx),函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$.
已知向量$\overrightarrow{a}$=($\sqrt{2}$sinx,$\frac{{\sqrt{2}}}{2}$(cosx+sinx)),$\overrightarrow{b}$=(2cosx,sinx-cosx),函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$.