题目内容
【题目】某地区现有一个直角梯形水产养殖区ABCD，∠ABC=90°，AB∥CD，AB=800m，BC=1600m，CD=4000m，在点P处有一灯塔（如图），且点P到BC，CD的距离都是1200m，现拟将养殖区ACD分成两块，经过灯塔P增加一道分隔网EF，在△AEF内试验养殖一种新的水产品，当△AEF的面积最小时，对原有水产品养殖的影响最小．设AE=d．
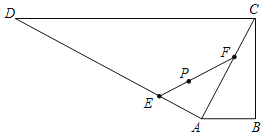
（1）若P是EF的中点，求d的值；
（2）求对原有水产品养殖的影响最小时的d的值，并求△AEF面积的最小值．
【答案】（1）480
; （2）对原有水产品养殖的影响最小时，d=480．△AEF面积的最小值为192000m2
【解析】
（1）建立平面坐标系，求出直线AD，AC的方程，根据P为EF的中点列方程得出E点坐标，从而可计算d；
（2）根据基本不等式得出AEAF的最小值，进而求出△AEF的面积最小值．
解：（1）以A为坐标原点，AB所在直线为x轴，建立如图所示的平面直角坐标系，
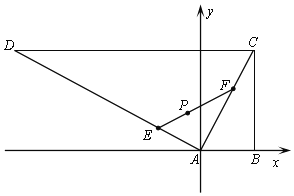
则C（800，1600），B（800，0），P（-400，400），D（-3200，1600）．
AC所在直线方程为y=2x，AD所在直线方程为y=-
x．
设E（-2m，m），F（n，2n），m＞0，＞0．
∵P是EF的中点，∴
，解得
，
∴E（-960，480），
∴d=|AE|=
=480．
（2）∵EF经过点P，∴kPE=kPF，
即
=
，化简得80m+240n=mn．
由基本不等式得：mn=80m+240n≥160
，
即mn≥76800，当且仅当m=3n=480时等号成立．
∵kACkAD=-1，∴AC⊥AD，
∴S△AEF=AEAF=
mn=
mn≥
76800=192000，
此时E（-960，480），d=AE=480．
故对原有水产品养殖的影响最小时，d=480．△AEF面积的最小值为192000m2．
