题目内容
【题目】在锐角△ABC中，
分别为A、B、C所对的边，且
（1）确定角C的大小；
（2）若c＝
，求△ABC周长的取值范围．
【答案】（1）C=60°；（2）（
+3
，
]．
【解析】
（1）利用正弦定理化简已知条件，求得
的值，根据三角形是锐角三角形求得
的大小.（2）利用正弦定理将
转化为角度来表示，求得三角形
周长的表达式，利用三角函数求取值范围的方法，求得三角形周长的取值范围.
解:（1）已知a、b、c分别为A、B、C所对的边，
由
a＝2csinA，
得sinA＝2sinCsinA，又sinA≠0，则sinC=
，
∴C=60°或C=120°,
∵△ABC为锐角三角形，∴C=120°舍去。∴C=60°
（2）∵c=，sinC=
∴由正弦定理得：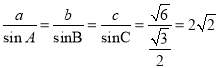
,
即a=2sinA，b=2sinB，又A+B=π-C=
，
即B=-A
∴a+b+c=2（sinA+sinB）+=2 [sinA+sin（-A）]+
=2（sinA+sincosA-cossinA）+
=2（sinAcos
+cosAsin）+=2sin（A+）+，
∵△ABC是锐角三角形，
∴＜A＜
，
∴＜sin（A+）≤1，
则△ABC周长的取值范围是（+3，]．
练习册系列答案
相关题目
【题目】为了了解学生的学习情况，一次测试中，科任老师从本班中抽取了n个学生的成绩（满分100分，且抽取的学生成绩均在
内）进行统计分析.按照
，
，
，
，
，
的分组作出频率分布直方图和频数分布表.
频数分布表 | |
| x |
| 4 |
| 10 |
| 12 |
| 8 |
| 4 |
（1）求n，a，x的值；
（2）在选取的样本中，从低于60分的学生中随机抽取两名学生，试问这两名学生在同一组的概率是多少？
