题目内容
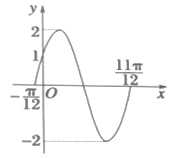
【题目】已知函数![]() ;
;
(1)当![]() 时,若
时,若![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若定义在![]() 上的奇函数
上的奇函数![]() 满足
满足![]() ,且当
,且当![]() ,
,![]() ,求
,求![]() 在
在![]() 上的解析式;
上的解析式;
(3)对于(2)中的![]() ,若关于
,若关于![]() 的不等式
的不等式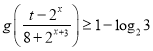 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据对数函数的真数部分大于0,及对数的运算性质,可将不等式化为![]() ,且
,且![]() 且
且![]() ,解不等式组可得
,解不等式组可得![]() 的取值范围;
的取值范围;
(2)利用奇偶性得出![]() ,
,![]() ,转化得出当
,转化得出当![]() 时,
时,![]() ,当
,当![]() 时,根据函数的奇偶性求解即可.
时,根据函数的奇偶性求解即可.
(3)关于![]() 的不等式关于
的不等式关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,等价于
上恒成立,等价于![]() 在
在![]() 上恒成立,即
上恒成立,即![]()
![]() ,分类讨论后,综合讨论结果,可得实数
,分类讨论后,综合讨论结果,可得实数![]() 的取值范围.
的取值范围.
解:(1)原不等式可化为![]() ,
,
![]() ,且
,且![]() ,且
,且![]() ,
,
得![]() .
.
(2)![]() ,
,![]() ,
,
所以![]() 的周期为:4,
的周期为:4,
![]() 当
当![]() 时,
时,![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
![]() 定义在
定义在![]() 上的奇函数
上的奇函数![]() ,
,
![]() ,即
,即![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
(3)![]() 关于
关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,
上恒成立,
![]() 记
记![]() ,
,
![]() 关于
关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,
上恒成立,
![]() 在
在![]() 上恒成立,
上恒成立,
当![]() 时,
时,![]() ,
,
![]()
![]() ,即
,即 解得
解得![]() .
.
当![]() ,即
,即![]() 时,
时,![]() ,
,![]() ,即
,即![]() 满足条件;
满足条件;
当![]() 时,
时,![]() ,
,
由![]() 在
在![]() 上恒成立,
上恒成立,
得![]() ,
,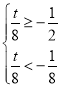 解得
解得![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目