Question

【题目】已知椭圆C1的方程为，双曲线C2的左、右焦点分别是C1的左、右顶点，而C2的左、右顶点分别是C1的左、右焦点，O为坐标原点．

(1)求双曲线C2的方程；

(2)若直线l：y＝kx＋与双曲线C2恒有两个不同的交点A和B，且，求k的取值范围．

Answer 1

【答案】（1）；（2）

【解析】试题分析：（1）由两曲线长轴与焦点关系，求出双曲线C2的方程。（2）设A(x1，y1)，B(x2，y2)，直线与双曲线组方程组，得到韦达定理关系，注意判别式控制参数k范围。把向量关系>2，坐标化即x1x2＋y1y2>2，代入韦达可求。

试题解析：(1)设双曲线C2的方程为

则a2＝4－1＝3，c2＝4，再由a2＋b2＝c2，得b2＝1，

故双曲线C2的方程为－y2＝1.

(2)将y＝kx＋代入－y2＝1，

得(1－3k2)x2－6kx－9＝0.

由直线l与双曲线C2交于不同的两点，

得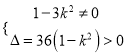

∴k2<1且k2≠.①

设A(x1，y1)，B(x2，y2)，

则x1＋x2＝，x1x2＝.

∴x1x2＋y1y2＝x1x2＋(kx1＋)(kx2＋)

＝(k2＋1)x1x2＋k(x1＋x2)＋2＝.

又∵>2，即x1x2＋y1y2>2，∴ >2 >2，即>0，

解得<k2<3.②

由①②得<k2<1，

故k的取值范围为