题目内容
在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60°
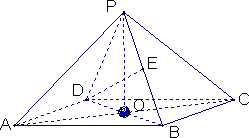
(1)求四棱锥P-ABCD的体积;
(2)若E是PB的中点,求异面直线DE与PA所成角的余弦值
答案:
解析:
解析:

练习册系列答案
相关题目
题目内容
在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60°

(1)求四棱锥P-ABCD的体积;
(2)若E是PB的中点,求异面直线DE与PA所成角的余弦值
