题目内容
 已知在四棱锥P一ABCD中,二面角P一AD一B为60°,∠PDA=45°,∠DAB=90°,∠PAD=90°,∠ADC=135°,
已知在四棱锥P一ABCD中,二面角P一AD一B为60°,∠PDA=45°,∠DAB=90°,∠PAD=90°,∠ADC=135°,(Ⅰ)求证:平面PAB⊥平面ABCD;
(Ⅱ)求PD与平面ABCD所成角的正弦值;
(Ⅲ)求二面角P一CD一B的正切值.
分析:(Ⅰ)要证明面面垂直,要在其中一个平面内找垂直于另一个平面的垂线,由已知可知,DA⊥PA且 DA⊥AB,所以DA⊥平面PAB,从而所证两面垂直
(Ⅱ)求线面所成的角,需要先找斜线在平面内的射影,由(Ⅰ)知,过P作AB的垂线PH,就垂直于平面ABCD,故∠PDH为PD为平面ABCD所成角,再在三角形PHD中计算该角即可
(Ⅲ)要求二面角,需先找到二面角的平面角,由于PH⊥平面ABCD,故可用三垂线法作出二面角的平面角,即过H作CD的垂线,垂足为F,则∠PFH为二面角P-CD-B的平面角,再在三角形PFH中计算此角的正切值即可
(Ⅱ)求线面所成的角,需要先找斜线在平面内的射影,由(Ⅰ)知,过P作AB的垂线PH,就垂直于平面ABCD,故∠PDH为PD为平面ABCD所成角,再在三角形PHD中计算该角即可
(Ⅲ)要求二面角,需先找到二面角的平面角,由于PH⊥平面ABCD,故可用三垂线法作出二面角的平面角,即过H作CD的垂线,垂足为F,则∠PFH为二面角P-CD-B的平面角,再在三角形PFH中计算此角的正切值即可
解答:解:(I)证明:∵∠DAB=90°∴DA⊥AB
∵∠PAD=90°∴DA⊥PA,∵PA∩AB=A
∴DA⊥平面PAB,∵DA?平面ABCD
∴平面PAB⊥平面ABCD
(II)∵平面PAB⊥平面ABCD,过P作PH⊥AB交于H,则PH⊥平面ABCD
连DH,则∠PDH为PD为平面ABCD所成角
∵DA⊥AB,DA⊥PA,∴∠PAB为二面角P-AD-B的平面角,∠PAB=60°
设PA=a,则AD=a,PD=
a,PH=
a,∴sin∠PDH=
=
=
则PD与平面ABCD所成角的正弦值为
(III)延长CD、BA交于E,过H作HF⊥CE于F,连PF,
∵PH⊥平面ABCD,∴PF⊥CE
∴∠PFH为二面角P-CD-B的平面角
∵∠ADC=135°,∴∠EDA=45°,则EA=AD=a,EH=
a,
∵∠E=45°
∴FH=EH•sin45°=
a•
=
a,
tan∠PFH=
=
=
∵∠PAD=90°∴DA⊥PA,∵PA∩AB=A
∴DA⊥平面PAB,∵DA?平面ABCD
∴平面PAB⊥平面ABCD
(II)∵平面PAB⊥平面ABCD,过P作PH⊥AB交于H,则PH⊥平面ABCD
连DH,则∠PDH为PD为平面ABCD所成角
∵DA⊥AB,DA⊥PA,∴∠PAB为二面角P-AD-B的平面角,∠PAB=60°
设PA=a,则AD=a,PD=
| 2 |
| ||
| 2 |
| PH |
| PD |
| ||||
|
| ||
| 4 |
则PD与平面ABCD所成角的正弦值为
| ||
| 4 |
(III)延长CD、BA交于E,过H作HF⊥CE于F,连PF,
∵PH⊥平面ABCD,∴PF⊥CE
∴∠PFH为二面角P-CD-B的平面角
∵∠ADC=135°,∴∠EDA=45°,则EA=AD=a,EH=
| 3 |
| 2 |
∵∠E=45°
∴FH=EH•sin45°=
| 3 |
| 2 |
| ||
| 2 |
3
| ||
| 4 |
tan∠PFH=
| PH |
| FH |
| ||||
|
| ||
| 3 |
点评:本题考查了空间面面垂直的证明方法,空间线面角的作法和求法,空间面面角的作法和求法,解题时要认真体会垂线在解题中的重要应用,还要注意规范解题过程,逻辑严密

练习册系列答案
相关题目
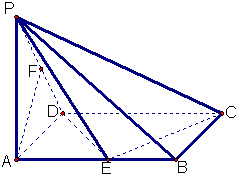 已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,
已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,
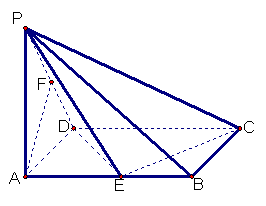
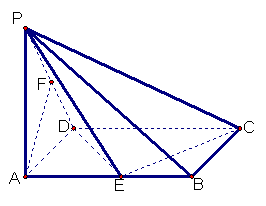 (13分)已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点。
(13分)已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点。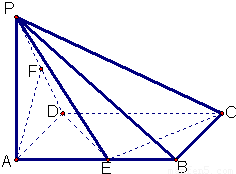 已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,
已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,