题目内容
 如图.在四棱锥P一ABCD中,底面ABCD是正方形,侧棱PD⊥底 面ABCD,PD=DC=2,E是PC的中点.
如图.在四棱锥P一ABCD中,底面ABCD是正方形,侧棱PD⊥底 面ABCD,PD=DC=2,E是PC的中点.(1)证明:PA∥平面EDB;
(2)证明:平面PAC⊥平面PDB;
(3)求三梭锥D一ECB的体积.
分析:(1)利用三角形的中位线和线面平行的判定定理即可证明;
(2)利用面面垂直的判定定理即可证明;
(3)取CD的中点F,连接EF,利用三角形的中位线定理可得EF⊥底面ABCD,由V三棱锥D-ECB=V三棱锥E-BCD即可求出体积.
(2)利用面面垂直的判定定理即可证明;
(3)取CD的中点F,连接EF,利用三角形的中位线定理可得EF⊥底面ABCD,由V三棱锥D-ECB=V三棱锥E-BCD即可求出体积.
解答:解:(1)证明:设AC∩BD=O,连接EO.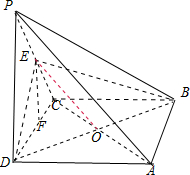
∵底面ABCD是正方形,∴点O是AC的中点,
在△PAC中,EO是中位线,∴EO∥PA.
∵PA?平面EDB,EO?平面EDB,
∴PA∥平面EDB.
(2)证明:∵底面ABCD是正方形,∴AC⊥BD,
∵PD⊥底面ABCD,∴PD⊥AC.
∵PD∩BD=D,∴AC⊥平面PBD,
∵AC?平面PAC,
∴平面PAC⊥平面PDB.
(3)取CD的中点F,连接EF,
则EF∥PD,EF=
PD=1,
∵PD⊥底面ABCD,
∴EF⊥底面ABCD.
∴V三棱锥D-ECB=V三棱锥E-BCD=
×
×22×1=
.

∵底面ABCD是正方形,∴点O是AC的中点,
在△PAC中,EO是中位线,∴EO∥PA.
∵PA?平面EDB,EO?平面EDB,
∴PA∥平面EDB.
(2)证明:∵底面ABCD是正方形,∴AC⊥BD,
∵PD⊥底面ABCD,∴PD⊥AC.
∵PD∩BD=D,∴AC⊥平面PBD,
∵AC?平面PAC,
∴平面PAC⊥平面PDB.
(3)取CD的中点F,连接EF,
则EF∥PD,EF=
| 1 |
| 2 |
∵PD⊥底面ABCD,
∴EF⊥底面ABCD.
∴V三棱锥D-ECB=V三棱锥E-BCD=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
点评:熟练掌握线面、面面的平行与垂直的判定定理和性质定理、三角形的中位线定理及等积变形是解题的关键.

练习册系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=1,AD=2,PA⊥底面ABCD,PD与底面成45°角,点E是PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=1,AD=2,PA⊥底面ABCD,PD与底面成45°角,点E是PD的中点. (2009•闸北区一模)如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥平面ABCD,AB=1,PA•AC=1,∠ABC=θ(0°<θ≤90°).
(2009•闸北区一模)如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥平面ABCD,AB=1,PA•AC=1,∠ABC=θ(0°<θ≤90°). (2013•兰州一模)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°
(2013•兰州一模)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60° (2013•青岛一模)如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,N是PB中点,过A、N、D三点的平面交PC于M.
(2013•青岛一模)如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,N是PB中点,过A、N、D三点的平面交PC于M. (2008•崇明县一模)(理科)如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PA⊥底面ABCD,PA=4,M为PA的中点,N为BC的中点.
(2008•崇明县一模)(理科)如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PA⊥底面ABCD,PA=4,M为PA的中点,N为BC的中点.