题目内容
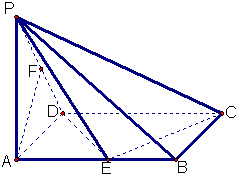 已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,
已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.
(Ⅰ)求证:AF∥平面PEC;
(Ⅱ)求PC与平面ABCD所成角的正切值;
(Ⅲ)求二面角P-EC-D的正切值.
分析:(Ⅰ)取PC的中点O,连接OF、OE.可得FO∥DC,且FO=
DC,又FO=AE.AF∥OE又OE?平面PEC,AF?平面PEC,可得线面平行.
(Ⅱ)PA⊥平面ABCD可得∠PCA是直线PC与平面ABCD所成的角.在Rt△PAC中,tan∠PCA=
.
(Ⅲ)作AM⊥CE,交CE的延长线于M.连接PM,得PM⊥CE,∴∠PMA是二面角P-EC-D的平面角tan∠PMA=
.
| 1 |
| 2 |
(Ⅱ)PA⊥平面ABCD可得∠PCA是直线PC与平面ABCD所成的角.在Rt△PAC中,tan∠PCA=
| ||
| 5 |
(Ⅲ)作AM⊥CE,交CE的延长线于M.连接PM,得PM⊥CE,∴∠PMA是二面角P-EC-D的平面角tan∠PMA=
| 2 |
解答:解:(Ⅰ)取PC的中点O,连接OF、OE.
∴FO∥DC,且FO=
DC
∴FO∥AE
又E是AB的中点.且AB=DC.
∴FO=AE.
∴四边形AEOF是平行四边形.
∴AF∥OE又OE?平面PEC,AF?平面PEC
∴AF∥平面PEC
(Ⅱ)连接AC
∵PA⊥平面ABCD,∴∠PCA是直线PC与平面ABCD所成的角
在Rt△PAC中,tan∠PCA=
=
=
即直线PC与平面ABCD所成的角正切为
(Ⅲ)作AM⊥CE,交CE的延长线于M.连接PM,
由三垂线定理,得PM⊥CE
∴∠PMA是二面角P-EC-D的平面角
由△AME∽△CBE,可得AM=
,
∴tan∠PMA=
=
∴二面角P一EC一D的正切为
∴FO∥DC,且FO=
| 1 |
| 2 |
∴FO∥AE
又E是AB的中点.且AB=DC.
∴FO=AE.
∴四边形AEOF是平行四边形.
∴AF∥OE又OE?平面PEC,AF?平面PEC
∴AF∥平面PEC
(Ⅱ)连接AC
∵PA⊥平面ABCD,∴∠PCA是直线PC与平面ABCD所成的角
在Rt△PAC中,tan∠PCA=
| PA |
| AC |
| 1 | ||
|
| ||
| 5 |
| ||
| 5 |
(Ⅲ)作AM⊥CE,交CE的延长线于M.连接PM,
由三垂线定理,得PM⊥CE
∴∠PMA是二面角P-EC-D的平面角
由△AME∽△CBE,可得AM=
| ||
| 2 |
∴tan∠PMA=
| PA |
| AM |
| 2 |
∴二面角P一EC一D的正切为
| 2 |
点评:解决成立问题的关键是将空间角找出并且把空间问题转化为平面问题,步骤是一作角二证角三求角四结论.

练习册系列答案
相关题目

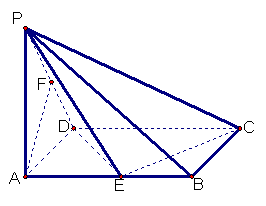
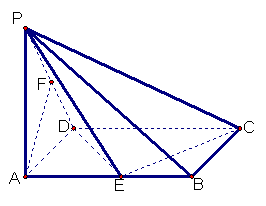 (13分)已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点。
(13分)已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点。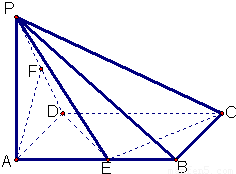 已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,
已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,