题目内容
18．
如图所示的复平面上的点A，B分别对应复数 z1，z2，则$\frac{{z}_{2}}{{z}_{1}}$=（ ）| A． | -2i | B． | 2i | C． | 2 | D． | -2 |
分析 由图求出z1，z2，代入$\frac{{z}_{2}}{{z}_{1}}$后利用复数代数形式的乘除运算化简求值．
解答 解：由图可知，z1=-1+i，z2=2+2i，
则$\frac{{z}_{2}}{{z}_{1}}=\frac{2+2i}{-1+i}=\frac{（2+2i）（-1-i）}{（-1+i）（-1-i）}=-（1+i）^{2}=-2i$．
故选：A．
点评 本题考查了复数的代数表示法及其几何意义，考查了复数代数形式的乘除运算，是基础题．
练习册系列答案
相关题目
9．某中学研究性学习小组，为了研究高中文科学生的历史成绩是否与语文成绩有关系，在本校高三年级随机调查了50名文科学生，调查结果表明：在语文成绩优秀的25人中16人历史成绩优秀，另外9人历史成绩一般；在语文成绩一般的25人中有6人历史成绩优秀，另外19人历史成绩一般．
（Ⅰ）试根据以上数据完成以下2×2列联表，并运用独立性检验思想，指出有多大把握认为高中文科学生的历史成绩与语文成绩有关系；
（Ⅱ）将其中某5名语文成绩与历史成绩均优秀的学生分别编号为1，2，3，4，5，某5名语文成绩优秀但历史成绩一般的学生也分别编号为1，2，3，4，5，从这两组学生中各任选1人进行学习交流，求被选取的2名学生的编号之和为3的倍数或4的倍数的概率．
参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
参考数据：
（Ⅰ）试根据以上数据完成以下2×2列联表，并运用独立性检验思想，指出有多大把握认为高中文科学生的历史成绩与语文成绩有关系；
| 语文成绩优秀 | 语文成绩一般 | 总计 | |
| 历史成绩优秀 | |||
| 历史成绩一般 | |||
| 总计 |
参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
参考数据：
| P（K2≥k0） | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
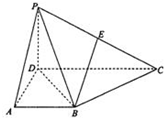在四棱锥P-ABCD中，侧面PCD⊥底面ABCD，PD⊥CD，E为PC中点，底面ABCD是直角梯形．AB∥CD，∠ADC=90°，AB=AD=PD=1，CD=2．