题目内容
6.若Sn=12-22+32-42…(-1)n-1•n2,则(n-6)•S2n+1的最小值为-90.分析 计算得S2n+1=2n2+3n+1,记f(n)=(n-6)•S2n+1=2n3-9n2-17n-6,问题转化为求函数f(x)=2x3-9x2-17x-6(x≥1)的最小值,解得当x=$\frac{9+\sqrt{183}}{6}$时取最小值,从而可得f(n)的最小值为-90.
解答 解:由题意可得S2n+1=12-22+32-42…-(2n)2+(2n+1)2
=-(1+2+3+4+…+2n-1+2n)+(2n+1)2
=-$\frac{2n(1+2n)}{2}$+(2n+1)2
=2n2+3n+1,
(n-6)•S2n+1=(n-6)•(2n2+3n+1)
=2n3-9n2-17n-6=f(n),
记f(x)=2x3-9x2-17x-6(x≥1),
令f′(x)=6x2-18x-17=0,解得x=$\frac{9±\sqrt{183}}{6}$,
所以f(x)在[1,$\frac{9+\sqrt{183}}{6}$)上单调递减,在($\frac{9+\sqrt{183}}{6}$,+∞)上单调递增,
又$\frac{9+\sqrt{183}}{6}$≈3.75,所以f(n)在n=3或n=4时取最小值,
f(3)=-84,f(4)=-90,所以f(n)的最小值为-90.
点评 本题考查数列的求和及数列的最值,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.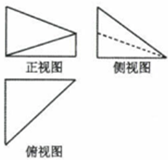 某几何体的三视图如图所示,其中正视图是两底边长分别为1,2的直角梯形,俯视图是斜边长为3的直角三角形,该几何体体积是( )
某几何体的三视图如图所示,其中正视图是两底边长分别为1,2的直角梯形,俯视图是斜边长为3的直角三角形,该几何体体积是( )
 某几何体的三视图如图所示,其中正视图是两底边长分别为1,2的直角梯形,俯视图是斜边长为3的直角三角形,该几何体体积是( )
某几何体的三视图如图所示,其中正视图是两底边长分别为1,2的直角梯形,俯视图是斜边长为3的直角三角形,该几何体体积是( )| A. | 1 | B. | 2 | C. | $\frac{7}{4}$ | D. | $\frac{9}{4}$ |
14.复数$\frac{1}{2-i}$的虚部为( )
| A. | $\frac{1}{5}i$ | B. | $\frac{1}{5}$ | C. | $\frac{\sqrt{5}}{5}i$ | D. | $\frac{\sqrt{5}}{5}$ |
1.已知复数z的共轭复数为$\overline{z}$,且$\overline{z}$=$\frac{2i}{1+i}$,则z在复平面内的对应点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18. 如图所示的复平面上的点A,B分别对应复数 z1,z2,则$\frac{{z}_{2}}{{z}_{1}}$=( )
如图所示的复平面上的点A,B分别对应复数 z1,z2,则$\frac{{z}_{2}}{{z}_{1}}$=( )
 如图所示的复平面上的点A,B分别对应复数 z1,z2,则$\frac{{z}_{2}}{{z}_{1}}$=( )
如图所示的复平面上的点A,B分别对应复数 z1,z2,则$\frac{{z}_{2}}{{z}_{1}}$=( )| A. | -2i | B. | 2i | C. | 2 | D. | -2 |