题目内容
某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关.现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,在将两组工人的日平均生产件数分成5组: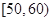 ,
,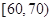 ,
, ,
,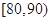 ,
,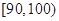 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.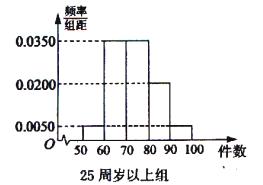
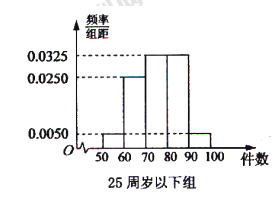

(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的频率.
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成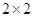 的列联表,并判断是否有
的列联表,并判断是否有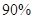 的把握认为“生产能手与工人所在的年龄组有关”?
的把握认为“生产能手与工人所在的年龄组有关”?
附表: 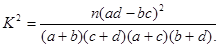
(1)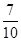 (2)没有
(2)没有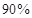 的把握认为“生产能手与工人所在的年龄组有关”
的把握认为“生产能手与工人所在的年龄组有关”
解析试题分析:(1)因为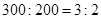 ,所以抽取的100名工人中
,所以抽取的100名工人中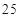 周岁以上组工人
周岁以上组工人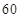 名,
名,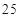 周岁以下组工人
周岁以下组工人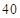 名。分别求出日平均生产件数不足
名。分别求出日平均生产件数不足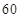 件的工人中,
件的工人中,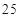 周岁以上组工人和
周岁以上组工人和 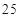 周岁以下组各有几人。然后用例举法将所有基本事件一一例举,根据古典概型概率公式可求其概率即其频率。(2)根据频率分布直方图完成
周岁以下组各有几人。然后用例举法将所有基本事件一一例举,根据古典概型概率公式可求其概率即其频率。(2)根据频率分布直方图完成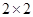 列联表,根据公式计算
列联表,根据公式计算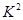 ,若
,若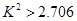 则说明有
则说明有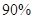 的把握认为“生产能手与工人所在的年龄组有关”,否则,无关。
的把握认为“生产能手与工人所在的年龄组有关”,否则,无关。
试题解析:解:(1)由已知得,样本中有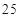 周岁以上组工人
周岁以上组工人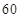 名,
名,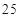 周岁以下组工人
周岁以下组工人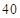 名
名
所以,样本中日平均生产件数不足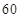 件的工人中,
件的工人中,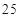 周岁以上组工人有
周岁以上组工人有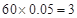 (人),
(人),
记为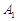 ,
,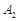 ,
,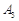 ;
;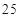 周岁以下组工人有
周岁以下组工人有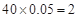 (人),记为
(人),记为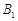 ,
,
从中随机抽取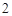 名工人,所有可能的结果共有
名工人,所有可能的结果共有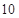 种,他们是:
种,他们是: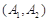 ,
,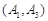 ,
,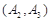 ,
,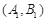 ,
,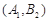 ,
,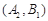 ,
,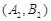 ,
,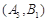 ,
,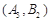 ,
,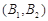
其中,至少有一名“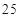 周岁以下组”工人的可能结果共有
周岁以下组”工人的可能结果共有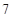 种,它们是:
种,它们是: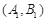 ,
,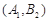 ,
,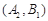 ,
,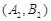 ,
,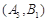 ,
,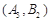 ,
,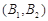 .故所求的概率:
.故所求的概率: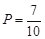
(2)由频率分布直方图可知,在抽取的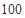 名工人中,“
名工人中,“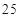 周岁以上组”中的生产能手
周岁以上组”中的生产能手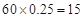 (人),“
(人),“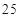 周岁以下组”中的生产能手
周岁以下组”中的生产能手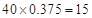 (人),据此可得
(人),据此可得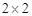 列联表如下:
列联表如下:
所以得: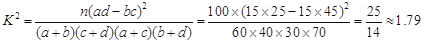
因为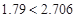 ,所以没有
,所以没有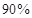 的把握认为“生产能手与工人所在的年龄组有关”
的把握认为“生产能手与工人所在的年龄组有关”
考点:1分层抽样;2频率分布直方图;3古典概型概率公式;4独立性检验。

从发生汽车碰撞事故的司机中抽取2 000名司机.根据他们的血液中是否含有酒精以及他们是否对事故负有责任.将数据整理如下:
| | 有责任 | 无责任 | 合计 |
| 有酒精 | 650 | 150 | 800 |
| 无酒精 | 700 | 500 | 1 200 |
| 合计 | 1 350 | 650 | 2 000 |
为了比较两种治疗失眠症的药(分别称为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者在服用一段时间后,记录他们日平均增加的睡眠时间(单位:h).试验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:
| 0.6 | 1.2 | 2.7 | 1.5 | 2.8 | 1.8 | 2.2 | 2.3 | 3.2 | 3.5 |
| 2.5 | 2.6 | 1.2 | 2.7 | 1.5 | 2.9 | 3.0 | 3.1 | 2.3 | 2.4 |
| 3.2 | 1.7 | 1.9 | 0.8 | 0.9 | 2.4 | 1.2 | 2.6 | 1.3 | 1.4 |
| 1.6 | 0.5 | 1.8 | 0.6 | 2.1 | 1.1 | 2.5 | 1.2 | 2.7 | 0.5 |
(2) 根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?
| A药 | | B药 |
| | 0. 1. 2. 3. | |
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
 =bx+a.
=bx+a.(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)


 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求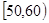 ,2;
,2;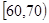 ,7;
,7;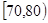 ,10;
,10;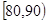 ,x;[90,100],2.其频率分布直方图受到破坏,可见部分如下图所示,据此解答如下问题.
,x;[90,100],2.其频率分布直方图受到破坏,可见部分如下图所示,据此解答如下问题.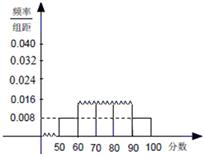
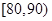 的矩形的高;
的矩形的高;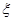 ,求
,求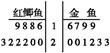
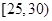 ,第2组
,第2组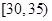 ,第3组
,第3组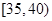 ,第4组
,第4组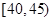 ,第5组
,第5组 ,得到的频率分布直方图如图所示,下表是年龄的频率分布表.
,得到的频率分布直方图如图所示,下表是年龄的频率分布表.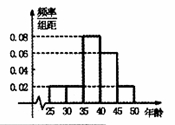

 的值;
的值;