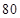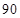题目内容
某电视台组织部分记者,用“10分制”随机调查某社区居民的幸福指数.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(1)指出这组数据的众数和中位数;
(2)若幸福指数不低于9.5分,则称该人的幸福指数为“极幸福”.求从这16人中随机选取3人,至多有1人是“极幸福”的概率;
(3)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求 的分布列及数学期望.
的分布列及数学期望.
(1)8.6,8.75;(2)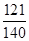 ;(3)参考解析
;(3)参考解析
解析试题分析:(1)由众数即为样本中出现次数最多的数字,中位数即为样本数据从小到大排序最中间的那个数字或是最中间的两个数字.根据所给的数字即可得到结论. 某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如下表: 大家知道,莫言是中国首位获得诺贝尔奖的文学家,国人欢欣鼓舞.某高校文学社从男女生中各抽取50名同学调查对莫言作品的了解程度,结果如下: 某批次的某种灯泡共 在某次数学考试中,抽查了1000名学生的成绩,得到频率分布直方图如图所示,规定85分及其以上为优秀.
(2)因为幸福指数不低于9.5分的共有4人,求从这16人中随机选取3人,至多有1人是“极幸福”的概率,转化为16人中一人是“极幸福”的概率加上没有人是“极幸福”的概率.通过计算即可得到所求的结论.
(3)若从该社区(人数很多)任选3人,记 表示抽到“极幸福”的人数,共有四种情况,并且分别求出各种情况的概率,从而得到数学期望值.
表示抽到“极幸福”的人数,共有四种情况,并且分别求出各种情况的概率,从而得到数学期望值.
试题解析:(1)众数:8.6;中位数:8.75 ;
(2)设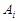 表示所取3人中有
表示所取3人中有 个人是“极幸福”,至多有1人是“极幸福”记为事件
个人是“极幸福”,至多有1人是“极幸福”记为事件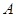 , 则
, 则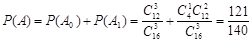 ;
;
(3)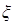 的可能取值为0,1,2,3.
的可能取值为0,1,2,3.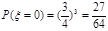 ;
;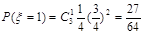 ;
;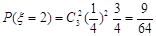 ;
;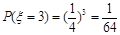 .
.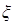 的分布列为:
的分布列为: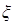

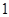
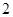


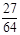
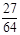
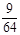
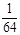
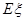
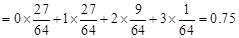 .
.
另解: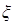 的可能取值为0,1,2,3,则
的可能取值为0,1,2,3,则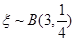 ,因此
,因此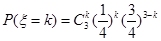 .
.
有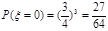 ;
;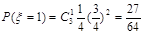 ;
;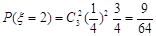 ;
;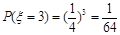 .
.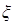 的分布列为:
的分布列为: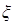



同步练习册全优达标测试卷系列答案
英才教程探究习案课时精练系列答案

初中语文阅读轻松组合周周练系列答案

剑桥小学英语系列答案
作业本江西教育出版社系列答案
新起点百分百单元测试卷系列答案
状元口算计算系列答案
题库精选系列答案
甲厂:
乙厂:分组
[29.86,29.90)
[29.90,29.94)
[29.94,29.98)
[29.9830.02),
[30.02,30.06)
[30.06,30.10)
[30.10,30.14)
频数
12
63
86
182
92
61
4
分组
[29.86,29.90)
[29.90,29.94)
[29.94,29.98)
[29.9830.02),
[30.02,30.06)
[30.06,30.10)
[30.10,30.14)
频数
29
71
85
159
76
62
18
(1)试分别估计两个分厂生产的零件的优质品率;
(2)由以上统计数据填下面2×2列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”?
附:
甲厂
乙厂
合计
优质品
非优质品
合 计
P(χ2≥x0)
0.05
0.01
x0
3.841
6.635
(1)试估计该校学生阅读莫言作品超过50篇的概率;阅读过莫言的
作品数(篇)
0~25
26~50
51~75
76~100
101~130
男生
3
6
11
18
12
女生
4
8
13
15
10
(2)对莫言作品阅读超过75篇的则称为“对莫言作品非常了解”,否则为“一般了解”.根据题意完成下表,并判断能否有75%的把握认为对莫言作品的非常了解与性别有关?
附:
非常了解
一般了解
合计
男生
女生
合计
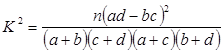
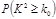
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
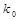
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
 个,对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于
个,对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于 天的灯泡是优等品,寿命小于
天的灯泡是优等品,寿命小于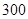 天的灯泡是次品,其余的灯泡是正品.
天的灯泡是次品,其余的灯泡是正品.
(1)根据频率分布表中的数据,写出寿命(天) 频数 频率 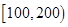


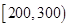


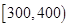


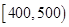
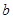
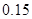
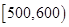

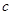
合计 

 、
、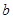 、
、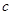 的值;
的值;
(2)某人从这 个灯泡中随机地购买了
个灯泡中随机地购买了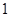 个,求此灯泡恰好不是次品的概率;
个,求此灯泡恰好不是次品的概率;
(3)某人从这批灯泡中随机地购买了 个,如果这
个,如果这 个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求
个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求 的最小值.
的最小值. 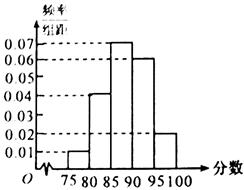
(1)下表是这次抽查成绩的频数分布表,试求正整数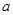 、
、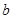 的值;
的值;
(2)现在要用分层抽样的方法从这1000人中抽取40人的成绩进行分析,求抽取成绩为优秀的学生人数;区间
[75,80)
[80,85)
[85,90)
[90,95)
[95,100]
人数
50
a
350
300
b
(3)在根据(2)抽取的40名学生中,要随机选取2名学生参加座谈会,记其中成绩为优秀的人数为X,求X的分布列与数学期望(即均值).
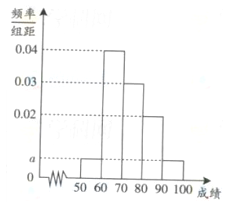

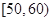 ,
,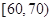 ,
, ,
,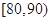 ,
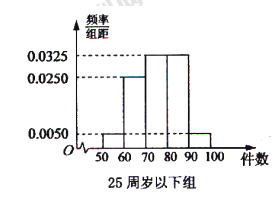
,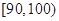 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.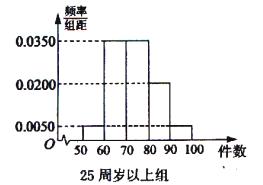
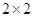 的列联表,并判断是否有
的列联表,并判断是否有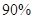 的把握认为“生产能手与工人所在的年龄组有关”?
的把握认为“生产能手与工人所在的年龄组有关”?
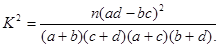
 次预赛成绩记录如下:
次预赛成绩记录如下: 

 乙
乙