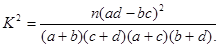题目内容
某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组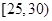 ,第2组
,第2组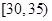 ,第3组
,第3组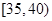 ,第4组
,第4组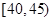 ,第5组
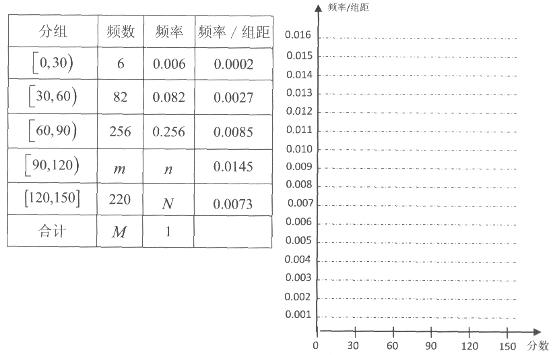
,第5组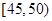 ,得到的频率分布直方图如图所示,下表是年龄的频率分布表.
,得到的频率分布直方图如图所示,下表是年龄的频率分布表.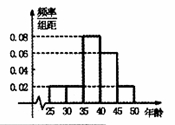

(1)求正整数 的值;
的值;
(2)现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组的人数分别是多少?
(3)在(2)的条件下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1人在第3组的概率.
(1)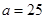 ,
,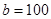 ,
,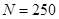 ;(2)第1,2,3组分别抽取1人,1人,4人;(3)
;(2)第1,2,3组分别抽取1人,1人,4人;(3) .
.
解析试题分析:本题主要考查频率分布直方图、分层抽样、随机事件的概率等数学知识,考查学生的分析问题解决问题的能力,考查学生的读图能力和计算能力.第一问,由频率分布直方图分析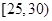 与
与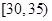 两组的人数相同,所以
两组的人数相同,所以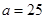 人,由于
人,由于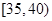 的高是
的高是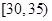 的4倍,所以
的4倍,所以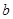 为100人;第二问,由第一问知,第1,2,3组共有150人,用分层抽样
为100人;第二问,由第一问知,第1,2,3组共有150人,用分层抽样 列出表达式,求出各层中需要抽取的人数;第三问,分别设出第1,2,3组抽取的人为
列出表达式,求出各层中需要抽取的人数;第三问,分别设出第1,2,3组抽取的人为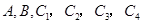 ,分别写出从6人中选取2人的情况共15种,在所有情况中选出符合题意的种数共8种,然后求概率.
,分别写出从6人中选取2人的情况共15种,在所有情况中选出符合题意的种数共8种,然后求概率.
试题解析:(1)由频率分布直方图可知,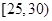 与
与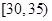 两组的人数相同,
两组的人数相同,
所以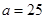 人. 1分
人. 1分
且 人. 2分
人. 2分
总人数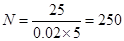 人. 3分
人. 3分
(2)因为第1,2,3组共有25+25+100=150人,利用分层抽样在150名员工中抽取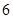 人,每组抽取的人数分别为:
人,每组抽取的人数分别为:
第1组的人数为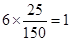 , 4分
, 4分
第2组的人数为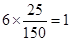 , 5分
, 5分
第3组的人数为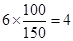 , 6分
, 6分
所以第1,2,3组分别抽取1人,1人,4人. 7分
(3)由(2)可设第1组的1人为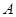 ,第2组的1人为
,第2组的1人为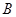 ,第3组的4人分别为
,第3组的4人分别为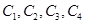 ,则从6人中抽取2人的所有可能结果为:
,则从6人中抽取2人的所有可能结果为: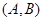 ,
,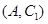 ,
,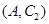 ,
,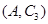 ,
, ,
,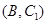 ,
,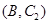 ,
,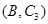 ,
,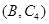 ,
,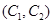 ,
, ,
,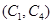 ,
,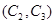 ,
,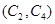 ,
,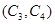 ,共有
,共有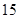 种. 9分
种. 9分
其中恰有1人年龄在第3组的所有结果为: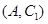 ,
,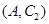 ,
,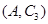 ,
, ,
,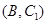 ,
,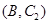 ,
,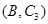 ,
,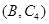 ,共有8种. 11分
,共有8种. 11分
所以恰有1人年龄在第3组的概率为 . 12分
. 12分
考点:1.频率分布直方图;2.分层抽样;3.随机事件的概率.

 通城学典默写能手系列答案
通城学典默写能手系列答案在某次数学考试中,抽查了1000名学生的成绩,得到频率分布直方图如图所示,规定85分及其以上为优秀.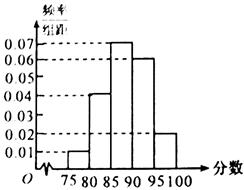
(1)下表是这次抽查成绩的频数分布表,试求正整数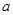 、
、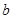 的值;
的值;
| 区间 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
| 人数 | 50 | a | 350 | 300 | b |
(3)在根据(2)抽取的40名学生中,要随机选取2名学生参加座谈会,记其中成绩为优秀的人数为X,求X的分布列与数学期望(即均值).
从某校高二年级 名男生中随机抽取
名男生中随机抽取 名学生测量其身高,据测量被测学生的身高全部在
名学生测量其身高,据测量被测学生的身高全部在 到
到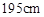 之间.将测量结果按如下方式分成
之间.将测量结果按如下方式分成 组:第一组
组:第一组 ,第二组
,第二组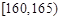 , ,第八组
, ,第八组 ,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.
,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.
频率分布表如下:
| 分组 | 频数 | 频率 | 频率/组距 |
| | | | |
 |  | 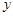 |  |
 |  |  |  |
| | | | |

(1)求频率分布表中所标字母的值,并补充完成频率分布直方图;
(2)若从身高属于第六组和第八组的所有男生中随机抽取
 名男生,记他们的身高分别为
名男生,记他们的身高分别为 ,求满足:
,求满足: 的事件的概率.
的事件的概率. 某工厂生产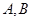 两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
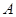 | 7 | 7 | 7.5 | 9 | 9.5 |
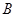 | 6 | 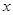 | 8.5 | 8.5 |  |
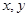 看不清,统计员只记得
看不清,统计员只记得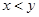 ,且
,且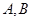 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.(Ⅰ)求表格中
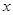 与
与 的值;
的值;(Ⅱ)若从被检测的5件
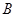 种元件中任取2件,求2件都为正品的概率.
种元件中任取2件,求2件都为正品的概率. 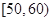 ,
,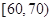 ,
, ,
,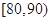 ,
,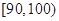 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.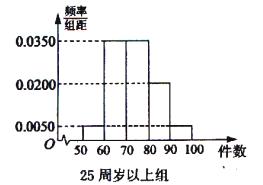
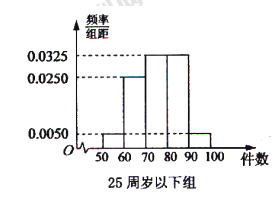
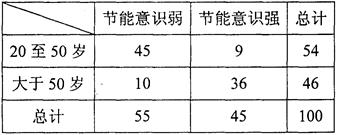
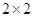 的列联表,并判断是否有
的列联表,并判断是否有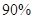 的把握认为“生产能手与工人所在的年龄组有关”?
的把握认为“生产能手与工人所在的年龄组有关”?