题目内容

已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0），经过点（3，-2）与向量（-1，1）平行的直线l交椭圆C于A，B两点，交x轴于M点，又
AM
=2
MB
．
（Ⅰ）求椭圆C长轴长的取值范围；
（Ⅱ）若|
AB
|=
3
2
2
，求椭圆C的方程．
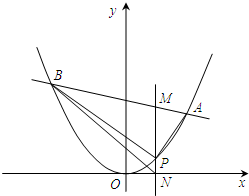
（I）设直线l与椭圆C交于A（x1，y1），B（x2，y2）两点，和x轴交于M（1，0）点．
由
AM
=2
MB
，知y1=-2y2，
将x=1-y代入
x2
a2
+
y2
b2
=1，得（a2+b2）y2-2b2y+b2（1-a2）=0，①
由韦达定理，知
y1+y2=
2b2
a2+b2
=-y2，②
y1y2=
b2(1-a2)
a2+b2
=-2y22，③

②2
③
得b2=
a2(1-a2)
a2-9
，④
对方程①由△=4b4-4b2（a2+b2）（1-a2）＞0，得a2+b2＞1．⑤
将④代入⑤，得a2+
a2(1-a2)
a2-9
＞1，解得1＜a2＜9，
又由a＞b及④，得a2＜5，∴1＜a2＜5，∴1＜a＜
5
．
∴所求椭圆长轴长的取值范围是（2，2
5
）．
（II）由（I）中②③得，
|AB|=
2
|y1-y2|=
2
•
(y1+y2)2-4y1y2

=
2
2
ab
a2+b2-1
a2+b2
，
∵|
AB
|=
3
2
2
，∴
2
2
ab
a2+b2-1
a2+b2
=
3
2
2
，⑥
联立④⑥，解得a2=3，b2=1，
∴椭圆C的方程为
x2
3
+y2=1．
练习册系列答案
相关题目
已知椭圆中心在原点，焦点在x轴上，长轴长等于12，离心率为
1
3
．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）在椭圆上任取一点P，过P点做y轴垂线段PQ，Q为垂足，当P在椭圆上运动时，求线段PQ的中点M的轨迹方程．
已知抛物线C：x2=2py过点P(1，
1
2
)，直线l交C于A，B两点，过点P且平行于y轴的直线分别与直线l和x轴相交于点M，N．
（1）求p的值；
（2）是否存在定点Q，当直线l过点Q时，△PAM与△PBN的面积相等？若存在，求出点Q的坐标；若不存在，请说明理由．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）有两个顶点在直线x+2y-2=0上
（1）求椭圆C的方程；
（2）当直线l：y=x+m与椭圆C相交时，求m的取值范围；
（3）设直线l：y=x+m与椭圆C交于A，B两点，O为坐标原点，若以为AB直径的圆过原点，求m的值．
已知抛物线C：x2=2py（p＞0）上一点A（m，4）到其焦点F的距离为
17
4
．
（1）求P与m的值；
（2）若直线l过焦点F交抛物线于P，Q两点，且|PQ|=5，求直线l的方程．
在平面直角坐标系xoy中，如图，已知椭圆
x2
9
+
y2
5
=1的左、右顶点为A、B，右焦点为F，设过点T（t，m）的直线TA、TB与此椭圆分别交于点M（x1，y1）、N（x2，y2），其中m＞0，y1＞0，y2＜0
（1）设动点P满足(
PF
+
PB
)(
PF
-
PB
)=13，求点P的轨迹方程；
（2）设x1=2，x2=
1
3
，求点T的坐标；
（3）若点T在点P的轨迹上运动，问直线MN是否经过x轴上的一定点，若是，求出定点的坐标；若不是，说明理由．
已知抛物线C：y2=4x的准线与x轴交于M点，过M点斜率为k的直线l与抛物线C交于A、B两点（A在M、B之间）．
（1）F为抛物线C的焦点，若|AM|=
5
4
|AF|，求k的值；
（2）如果抛物线C上总存在点Q，使得QA⊥QB，试求k的取值范围．
已知点M（-1，0），N（1，0），动点P（x，y）满足：|PM|•|PN|=
4
1+cos∠MPN
，
（1）求P的轨迹C的方程；
（2）是否存在过点N（1，0）的直线l与曲线C相交于A、B两点，并且曲线C存在点Q，使四边形OAQB为平行四边形？若存在，求出平行四边形OAQB的面积；若不存在，说明理由．
已知双曲线
x2
a2
-
y2
b2
=1(a＞0，b＞0)过点(
3
，
2
2
)，它的离心率为
6
2
，P、Q分别在双曲线的两条渐近线上，M是线段PQ中点，|PQ|=2
2
．
（Ⅰ）求双曲线及其渐近线方程；
（Ⅱ）求点M的轨迹C的方程；
（Ⅲ）过C左焦点F1的直线l与C相交于点A、B，F2为C的右焦点，求△ABF2面积最大时
F2A
•
F2B
的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网