题目内容
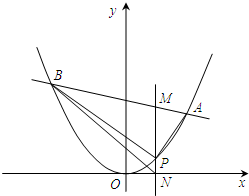
已知抛物线C:x2=2py过点P(1,
),直线l交C于A,B两点,过点P且平行于y轴的直线分别与直线l和x轴相交于点M,N.
(1)求p的值;
(2)是否存在定点Q,当直线l过点Q时,△PAM与△PBN的面积相等?若存在,求出点Q的坐标;若不存在,请说明理由.
| 1 |
| 2 |
(1)求p的值;
(2)是否存在定点Q,当直线l过点Q时,△PAM与△PBN的面积相等?若存在,求出点Q的坐标;若不存在,请说明理由.

(1)∵P(1,
)在抛物线C上,∴1=2p•
,得p=1.…(3分)
(2)假设存在定点Q,设A(x1,y1),B(x2,y2),AB的方程为y=kx+b.
联立
得x2-2kx-2b=0,
当△=4k2+8b>0时,有x1+x2=2k,x1x2=-2b.…(6分)
∴(x1-1)(x2-1)=x1x2-(x1+x2)+1=-2b-2k+1(*)
由题意知,N(1,0),M(1,k+b),
因为△PAM与△PBN的面积相等,所以
|PN|•|1-x2|=
|PM|•|1-x1|,
即|1-x2|=2|k+b-
|•|x1-1|,
也即|1-x2|=|2k+2b-1|•|x1-1|…(10分)
根据(*)式,得(x1-1)2=1,解得x1=0或x1=2.
所求的定点Q即为点A,
即l过Q(0,0)或Q(2,2)时,满足条件.…(14分)
| 1 |
| 2 |
| 1 |
| 2 |
(2)假设存在定点Q,设A(x1,y1),B(x2,y2),AB的方程为y=kx+b.
联立
|
当△=4k2+8b>0时,有x1+x2=2k,x1x2=-2b.…(6分)
∴(x1-1)(x2-1)=x1x2-(x1+x2)+1=-2b-2k+1(*)
由题意知,N(1,0),M(1,k+b),
因为△PAM与△PBN的面积相等,所以
| 1 |
| 2 |
| 1 |
| 2 |
即|1-x2|=2|k+b-
| 1 |
| 2 |
也即|1-x2|=|2k+2b-1|•|x1-1|…(10分)
根据(*)式,得(x1-1)2=1,解得x1=0或x1=2.
所求的定点Q即为点A,
即l过Q(0,0)或Q(2,2)时,满足条件.…(14分)

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目




