题目内容
(12分)已知函数 满足
满足 .
.
(1)设 ,求
,求 在
在 的上的值域;
的上的值域;
(2)设 ,在
,在 上是单调函数,求
上是单调函数,求 的取值范围.
的取值范围.
 满足
满足 .
.(1)设
 ,求
,求 在
在 的上的值域;
的上的值域;(2)设
 ,在
,在 上是单调函数,求
上是单调函数,求 的取值范围.
的取值范围.(1)值域为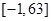 ; (2)
; (2) 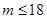 或
或 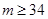 。
。
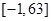 ; (2)
; (2) 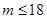 或
或 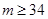 。
。本试题主要是考查了函数的单调性和值域的求解的综合运用。
(1)因为 ,那么
,那么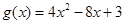
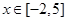 ,利用二次函数的性质可知函数的单调区间,进而得到值域。
,利用二次函数的性质可知函数的单调区间,进而得到值域。
(2)因为 ,在
,在 上是单调函数,,因此定义域在对称轴的一侧,可以解得。
上是单调函数,,因此定义域在对称轴的一侧,可以解得。
解:(1)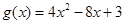
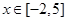
∵对称轴为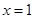 ∴值域为
∴值域为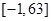
(2)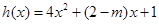
∵对称轴为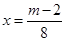 ∴
∴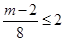 或
或 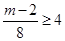 即
即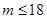 或
或 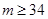
(1)因为
 ,那么
,那么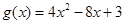
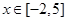 ,利用二次函数的性质可知函数的单调区间,进而得到值域。
,利用二次函数的性质可知函数的单调区间,进而得到值域。(2)因为
 ,在
,在 上是单调函数,,因此定义域在对称轴的一侧,可以解得。
上是单调函数,,因此定义域在对称轴的一侧,可以解得。解:(1)
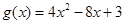
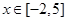
∵对称轴为
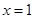 ∴值域为
∴值域为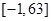
(2)
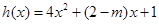
∵对称轴为
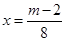 ∴
∴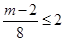 或
或 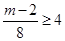 即
即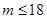 或
或 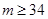

练习册系列答案
相关题目
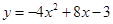
 , 若
, 若 ,则
,则 ( )
( )  或3
或3 ,
, ,
, 的最小值为
的最小值为 .
. ,若
,若 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;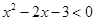 的解集为
的解集为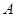 ,不等式
,不等式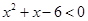 的解集为
的解集为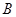 。
。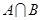 ;
; 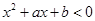 的解集为
的解集为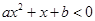 的解集。
的解集。 的值域为 。
的值域为 。 
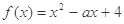 ,若
,若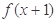 是偶函数,则实数
是偶函数,则实数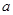 的值为( )
的值为( )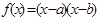 (其中
(其中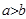 )的图象如图1所示,则函数
)的图象如图1所示,则函数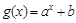 的图象是图2中的:
的图象是图2中的:
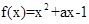 在区间
在区间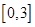 上有最小值-2,求实数a 的值
上有最小值-2,求实数a 的值