题目内容
【题目】已知抛物线![]() 上横坐标为
上横坐标为![]() 的点到焦点的距离为
的点到焦点的距离为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若过点![]() 的直线与抛物线交于不同的两点
的直线与抛物线交于不同的两点![]() ,且以
,且以![]() 为直径的圆过坐标原点
为直径的圆过坐标原点![]() ,求
,求![]() 的面积。
的面积。
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由抛物线![]() 上横坐标为
上横坐标为![]() 的点到焦点的距离为
的点到焦点的距离为![]() 可得
可得![]() 解得
解得![]() ,从而可得抛物线
,从而可得抛物线![]() 的方程;(2)先讨论直线斜率不存在时的情况,当斜率存在时,设直线方程为
的方程;(2)先讨论直线斜率不存在时的情况,当斜率存在时,设直线方程为![]() 联立
联立![]() ,消去
,消去![]() 得
得 ![]() ,根据韦达定理、平面向量数量积公式以及弦长公式、点到直线距离公式与三角形面积公式可求得
,根据韦达定理、平面向量数量积公式以及弦长公式、点到直线距离公式与三角形面积公式可求得![]() 的面积.
的面积.
试题解析:(1)依题意: ![]() 解得
解得![]() ,所以抛物线的方程为
,所以抛物线的方程为![]()
(2)依题意:若直线斜率不存在时,直线与抛物线只有一个交点,不符合题意;
所以设直线方程为![]()
联立![]() ,消去
,消去![]() 得
得 ![]()
所以![]()
又![]()
因为以![]() 为直径的圆过坐标原点,所以
为直径的圆过坐标原点,所以![]() ,
, ![]()
所以![]()
![]()
![]()
解得![]() ,由
,由![]() ,点
,点![]() 到直线
到直线![]() 的距离为
的距离为![]()
所以![]() 。
。

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
【题目】在某城市气象部门的数据中,随机抽取100天的空气质量指数的监测数据如表:
空气质量指数t | (0,50] | (50,100] | (100,150] | (150,200) | (200,300] | (300,+∞) |
质量等级 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 严重污染 |
天数K | 5 | 23 | 22 | 25 | 15 | 10 |
(1)若该城市各医院每天收治上呼吸道病症总人数y与当天的空气质量![]() (
(![]() 取整数)存在如下关系
取整数)存在如下关系![]() 且当t>300时,y>500,估计在某一医院收治此类病症人数超过200人的概率;
且当t>300时,y>500,估计在某一医院收治此类病症人数超过200人的概率;
(2)若在(1)中,当t>300时,y与t的关系拟合的曲线为![]() ,现已取出了10对样本数据(ti,yi)(i=1,2,3,…,10),且知
,现已取出了10对样本数据(ti,yi)(i=1,2,3,…,10),且知![]()
![]() 试用可线性化的回归方法,求拟合曲线的表达式.(附:线性回归方程
试用可线性化的回归方法,求拟合曲线的表达式.(附:线性回归方程![]() 中,
中, 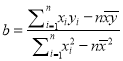 ,
, ![]() .)
.)