题目内容
如图,四棱锥S- ABCD中,底面ABCD为平行四边形,E是SA上一点,试探求点E的位置,使SC//平面EBD,并证明.

答:点E的位置是 .
证明:

答:点E的位置是 .
证明:
 中点
中点点E的位置是棱SA的中点 .
证明:取SA的中点E,连结EB,ED,AC,设AC与BD的交点为O,连结EO.
∵四边形ABCD是平行四边形,
∴点O是AC的中点.
又E是SA的中点,∴OE是ΔSAC的中位线.
∴OE//SC.
∵SC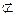 平面EBD,OE
平面EBD,OE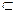 平面EBD,
平面EBD,
∴SC//平面EBD.
证明:取SA的中点E,连结EB,ED,AC,设AC与BD的交点为O,连结EO.
∵四边形ABCD是平行四边形,
∴点O是AC的中点.
又E是SA的中点,∴OE是ΔSAC的中位线.
∴OE//SC.
∵SC
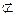 平面EBD,OE
平面EBD,OE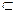 平面EBD,
平面EBD,∴SC//平面EBD.

练习册系列答案
相关题目
 .
.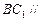 平面
平面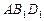 ;
;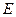 、
、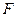 分别是
分别是 的中点,则
的中点,则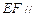 平面
平面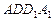 .
.
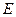 、
、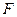 分别是正方体
分别是正方体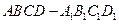 的棱
的棱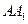 和棱
和棱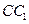 的中点.
的中点.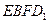 的形状;
的形状;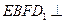 平面
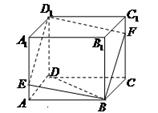
平面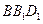 .
.
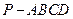 中,底面
中,底面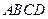 是边长为
是边长为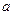 的正方形,侧面
的正方形,侧面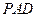
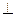 底面
底面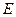 、
、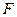 分别为
分别为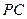 、
、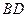 的中点.
的中点.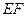 //平面
//平面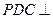 平面
平面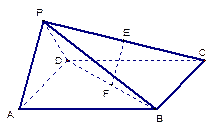
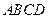 中,
中,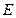 ,
,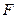 分别是
分别是 ,
,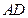 的中点.
的中点.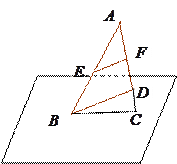 求证:
求证: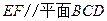
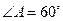
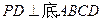
 平面PAD;
平面PAD;
 、
、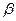 ,则下列说法中正确的是 ( )
,则下列说法中正确的是 ( )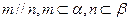 ,则
,则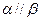
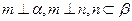 ,则
,则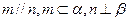 ,则
,则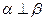
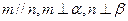 ,则
,则