题目内容
17.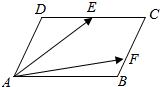 如图,平行四边形ABCD中,E为CD中点,F在线段BC上,且BC=3BF.已知$\overrightarrow{AD}$=x$\overrightarrow{AE}$+y$\overrightarrow{AF}$,则x的值为$\frac{6}{5}$.
如图,平行四边形ABCD中,E为CD中点,F在线段BC上,且BC=3BF.已知$\overrightarrow{AD}$=x$\overrightarrow{AE}$+y$\overrightarrow{AF}$,则x的值为$\frac{6}{5}$.
分析 根据平面向量的运算法则以及平行四边形中的向量相等,容易得到$\overrightarrow{AD}=\overrightarrow{BC}$,利用三角形法则得到向量$\overrightarrow{AD}$用$\overrightarrow{AE}$、$\overrightarrow{AF}$表示.
解答 解:$\overrightarrow{AD}=\overrightarrow{AE}+\overrightarrow{ED}$=$\overrightarrow{AE}+\frac{1}{2}\overrightarrow{CD}$=$\overrightarrow{AE}+\frac{1}{2}\overrightarrow{BA}$=$\overrightarrow{AE}+\frac{1}{2}(\overrightarrow{FA}-\overrightarrow{FB})$=$\overrightarrow{AE}+\frac{1}{2}\overrightarrow{FA}-\frac{1}{6}\overrightarrow{CB}$=$\overrightarrow{AE}-\frac{1}{2}\overrightarrow{AF}+\frac{1}{6}\overrightarrow{AD}$,
所以$\frac{5}{6}\overrightarrow{AD}=\overrightarrow{AE}-\frac{1}{2}\overrightarrow{AF}$,
所以$\overrightarrow{AD}=\frac{6}{5}\overrightarrow{AE}-\frac{3}{5}\overrightarrow{AF}$,
所以x=$\frac{6}{5}$;
故答案为:$\frac{6}{5}$.
点评 本题考查了平面向量的三角形法则以及平面向量基本定理的应用.属于中档题.

 53随堂测系列答案
53随堂测系列答案| A. | an=2n+1 | B. | an=2n-1 | C. | an=2n-3 | D. | an=2n+3 |
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{2}$ |
 用描述法表示下图所示阴影部分的点(包括边界上的点)的坐标的集合是( )
用描述法表示下图所示阴影部分的点(包括边界上的点)的坐标的集合是( )| A. | {-2≤x≤0且-2≤y≤0} | B. | {(x,y)|-2≤x≤0且-2≤y≤0} | ||
| C. | {(x,y)|-2≤x≤0且-2≤y<0} | D. | {(x,y)|-2≤x≤0或-2≤y≤0} |