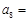题目内容
设数列 满足
满足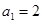 ,
, 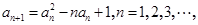
(1)求 ;
;
(2)猜想出 的一个通项公式并用数学归纳法证明你的结论.
的一个通项公式并用数学归纳法证明你的结论.
 满足
满足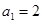 ,
, 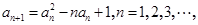
(1)求
 ;
;(2)猜想出
 的一个通项公式并用数学归纳法证明你的结论.
的一个通项公式并用数学归纳法证明你的结论.解:(1)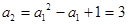
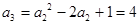 ,
,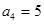 .
.
(2)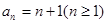 .
.
下面用数学归纳法证明如下:
①当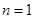 时,
时,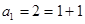 ,等式成立.
,等式成立.
②假设当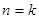 时等式成立,即
时等式成立,即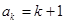 ,那么
,那么 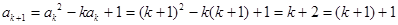 也就是说,当
也就是说,当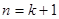 时,
时,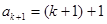 也成立. 根据(1)、(2)对于所有
也成立. 根据(1)、(2)对于所有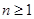 ,有
,有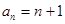 .
.
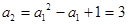
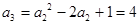 ,
,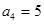 .
. (2)
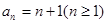 .
. 下面用数学归纳法证明如下:
①当
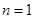 时,
时,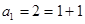 ,等式成立.
,等式成立. ②假设当
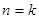 时等式成立,即
时等式成立,即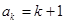 ,那么
,那么 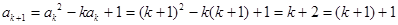 也就是说,当
也就是说,当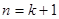 时,
时,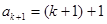 也成立. 根据(1)、(2)对于所有
也成立. 根据(1)、(2)对于所有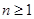 ,有
,有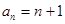 .
. 本试题主要是考查了数列的递推关系的运用,以及根据数学归纳法加以证明猜想的结论的综合运用。分为两步骤,注意证明过程中必须要用到假设。

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
 ,则
,则 是这个数列的 ( )
是这个数列的 ( ) 项
项 项
项 项
项 项
项 ,[ an]表示an的整数部分,(an)表示an的小数部分,an+1="[" an]+
,[ an]表示an的整数部分,(an)表示an的小数部分,an+1="[" an]+ (
( ),数列{bn}中,b1=1,b2=2,
),数列{bn}中,b1=1,b2=2, (
( ),则a1b1+ a2b2+…+anbn=
),则a1b1+ a2b2+…+anbn= 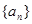 满足递推式
满足递推式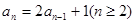 ,其中
,其中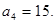
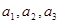 ;
;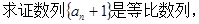 并求数列
并求数列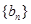 有
有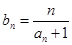 求数列
求数列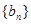 的前n项和
的前n项和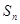 .
.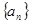 的通项公式为
的通项公式为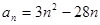 ,则数列
,则数列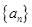 是各项均不为
是各项均不为 的等差数列,公差为
的等差数列,公差为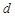 ,
,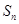 为其前
为其前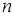 项和,且满足
项和,且满足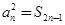 ,
,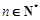 .数列
.数列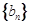 满足
满足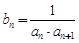 ,
,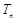 为数列
为数列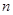 项和.
项和.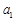 、
、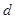 和
和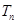 ;
;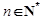 ,不等式
,不等式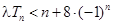 恒成立,求实数
恒成立,求实数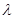 的取值范围;
的取值范围;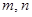
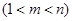 ,使得
,使得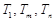 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有 ,则
,则 = .
= .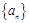 的前
的前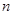 项和为
项和为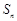 ,若
,若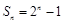 ,则
,则