题目内容
【题目】设自然数![]() 。求证:全体不大于n的合数可重新排列(不一定按原来的大小顺序排列),使得每三个依次相邻的数都有大于1的公因数(例如,当
。求证:全体不大于n的合数可重新排列(不一定按原来的大小顺序排列),使得每三个依次相邻的数都有大于1的公因数(例如,当![]() 时,排列
时,排列![]() 就满足要求)。
就满足要求)。
【答案】见解析
【解析】
对于![]() ,下面构造一种排列,使之满足要求.
,下面构造一种排列,使之满足要求.
令![]() 为所有的小于或等于
为所有的小于或等于![]() 的奇质数.因为
的奇质数.因为![]() ,所以
,所以![]() ,即
,即![]() .令
.令![]() x为合数,且x为
x为合数,且x为![]() 的奇数倍数}
的奇数倍数}![]() ,
,
![]() ,
,
特别地,![]() .
.
C={x![]() 是小于或等于n的偶合数,且
是小于或等于n的偶合数,且![]() .
.
我们再证明如下两个事实:
(1)![]()
(2) ![]() 及
及![]() .
.
因为![]() ,所以
,所以![]() ,且
,且![]() ,从而
,从而![]() ,即
,即![]() .故(1)得证.
.故(1)得证.
因为n≥25.所以,![]() .从而,
.从而,![]() .
.
又![]() 均为奇数.所以,
均为奇数.所以,![]() ,从而,
,从而,![]() (它等价于
(它等价于![]() ).故(2)得证.
).故(2)得证.
由(1)(2)可知把全体不大于n的合数组成如下的一个排列:![]()
![]()
容易验证:排列①中各数两两不相等,它们恰是不大于n的全体合数且每三个依次相邻的数都有大于1的公因数.故本题得证.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
【题目】某网红直播平台为确定下一季度的广告投入计划,收集了近6个月广告投入量![]() (单位:万元)和收益
(单位:万元)和收益![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
广告投入量/万元 | 2 | 4 | 6 | 8 | 10 | 12 |
收益/万元 | 14.21 | 20.31 | 31.8 | 31.18 | 37.83 | 44.67 |
用两种模型①![]() ,②
,②![]() 分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
|
|
|
|
7 | 30 | 1464.24 | 364 |
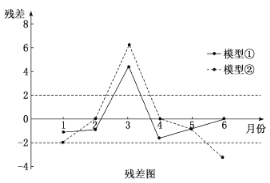
(1)根据残差图,比较模型①,②的拟合效果,应选择哪个模型?并说明理由.
(2)残差绝对值大于2的数据被认为是异常数据,需要剔除:
(i)剔除的异常数据是哪一组?
(ii)剔除异常数据后,求出(1)中所选模型的回归方程;
(iii)广告投入量![]() 时,(ii)中所得模型收益的预报值是多少?
时,(ii)中所得模型收益的预报值是多少?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: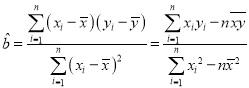 ,
,![]() .
.