题目内容
【题目】某网红直播平台为确定下一季度的广告投入计划,收集了近6个月广告投入量![]() (单位:万元)和收益
(单位:万元)和收益![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
广告投入量/万元 | 2 | 4 | 6 | 8 | 10 | 12 |
收益/万元 | 14.21 | 20.31 | 31.8 | 31.18 | 37.83 | 44.67 |
用两种模型①![]() ,②
,②![]() 分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
|
|
|
|
7 | 30 | 1464.24 | 364 |
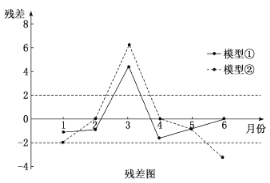
(1)根据残差图,比较模型①,②的拟合效果,应选择哪个模型?并说明理由.
(2)残差绝对值大于2的数据被认为是异常数据,需要剔除:
(i)剔除的异常数据是哪一组?
(ii)剔除异常数据后,求出(1)中所选模型的回归方程;
(iii)广告投入量![]() 时,(ii)中所得模型收益的预报值是多少?
时,(ii)中所得模型收益的预报值是多少?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: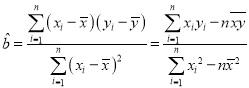 ,
,![]() .
.
【答案】(1)模型①,理由见解析;(2)(i)是3月份的数据; (ii)![]() ; (iii)62.04万元.
; (iii)62.04万元.
【解析】
(1)根据残差图中体现出的残差点分布,结合其均匀程度以及带状区域的宽窄,即可分析比较;
(2)(i)根据题意,结合残差图,即可求得![]() 月份的数据异常,应该剔除;
月份的数据异常,应该剔除;
(ii)根据已知数据和![]() 月份的数据,结合
月份的数据,结合![]() 和
和![]() 的计算公式,即可求得结果;
的计算公式,即可求得结果;
(iii)令![]() ,代入(ii)中所求回归直线方程,即可求得结果.
,代入(ii)中所求回归直线方程,即可求得结果.
(1)应该选择模型①,因为模型①的残差点比较均匀地落在水平的带状区域中,
且模型①的带状区域比模型②的带状区域窄,
所以模型①的拟合精度高,回归方程的预报精度高.
(2)(i)剔除异常数据是3月份的数据,即![]() ;
;
(ii)剔除异常数据,即3月份的数据后,得
![]() ,
,
![]()
![]() ,
,
![]() .
.
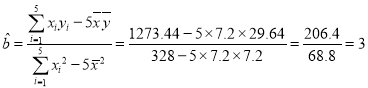 ,
,![]() .
.
所以![]() 关于
关于![]() 的回归方程为
的回归方程为![]() .
.
(iii)把![]() 代入(i)中所求回归方程得
代入(i)中所求回归方程得
![]() ,
,
故预报值为62.04万元.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案【题目】某同学的父亲决定今年夏天卖西瓜赚钱,根据去年6月份的数据统计连续五天内每天所卖西瓜的个数与温度之间的关系如下表:
温度 | 32 | 33 | 35 | 37 | 38 |
西瓜个数 | 20 | 22 | 24 | 30 | 34 |
(1)求这五天内所卖西瓜个数的平均值和方差;
(2)求变量![]() 之间的线性回归方程,并预测当温度为
之间的线性回归方程,并预测当温度为![]() 时所卖西瓜的个数.
时所卖西瓜的个数.
附: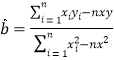 ,
,![]() (精确到
(精确到![]() ).
).

