题目内容

已知P是曲线y=2x2-1上的动点，定点A（0，-1），且点P不同于点A，若M点满足
PM
=2
MA
，求点M的轨迹方程．
由题意，设P（x0，y0），M（x，y），
∵
PM
=2
MA
，定点A（0，-1），
∴（x-x0，y-y0）=2（-x，-1-y），
∴x0=3x，y0=3y+2；
∵P是抛物线y=2x2-1上的动点，∴y0=2x02-1，
∴y=6x2-1．
故答案为：y=6x2-1．
练习册系列答案
相关题目
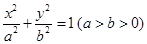已知椭圆G：过点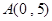，，C、D在该椭圆上，直线CD过原点O，且在线段AB的右下侧．
（1）求椭圆G的方程；
（2）求四边形ABCD 的面积的最大值．
在平面直角坐标系xOy中，点P到两点（0，-
3
），（0，
3
）的距离之和等于4，设点P的轨迹为C．
（1）写出C的方程；
（2）设直线y=kx+1与C交于A，B两点．k为何值时以AB为直径的圆经过原点O？此时|AB|的值是多少？
F1、F2是定点，|F1F2|=6，动点M满足|MF1|+|MF2|=6，则点M的轨迹是（　　）
A．椭圆B．直线C．线段D．圆
矩形ABCD的四个顶点的坐标分别为A（-2，1），B（2，1），C（2，-1），D（-2，-1），过原点且互相垂直的两条直线分别与矩形的边相交于E、F、G、H四点，则四边形EGFH的面积的最小值为______，最大值为______．
如图，P是抛物线C：y=
1
2
x2上一点，直线l过点P且与抛物线C交于另一点Q．
（Ⅰ）若直线l与过点P的切线垂直，求线段PQ中点M的轨迹方程；
（Ⅱ）若直线l不过原点且与x轴交于点S，与y轴交于点T，试求
|ST|
|SP|
+
|ST|
|SQ|
的取值范围．
已知定点A(-
3
，0)，B(
3
，0)，动点P（x，y）满足：||AP|-|BP||=2；
（1）求动点P的轨迹方程；
（2）直线mx-y+1=0与动点P的轨迹只有一个交点，求实数m的值．
已知点F1（-1，0），F2（1，0），动点G满足|GF1|+|GF2|=2
2
．
（Ⅰ）求动点G的轨迹Ω的方程；
（Ⅱ）已知过点F2且与x轴不垂直的直线l交（Ⅰ）中的轨迹Ω于P、Q两点．在线段OF2上是否存在点M（m，0），使得以MP，MQ为邻边的平行四边形是菱形？若存在，求实数m的取值范围；若不存在，请说明理由．
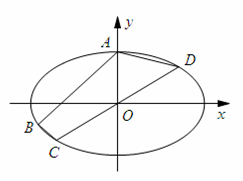
已知F是椭圆C的一个焦点，B是短轴的一个端点，线段BF的延长线交C于点D，且＝2，则C的离心率为________．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网