题目内容
如图所示,f(x)是定义在区间[-c,c](c>0)上的奇函数,令g(x)=af(x)+b,并有关于函数g(x)的四个论断:
①若a>0,对于[-1,1]内的任意实数m,n(m<n),
>0恒成立;
②函数g(x)是奇函数的充要条件是b=0;
③若a≥1,b<0,则方程g(x)=0必有3个实数根;
④?a∈R,g(x)的导函数g′(x)有两个零点;
其中所有正确结论的序号是______.

①若a>0,对于[-1,1]内的任意实数m,n(m<n),
| g(n)-g(m) |
| n-m |
②函数g(x)是奇函数的充要条件是b=0;
③若a≥1,b<0,则方程g(x)=0必有3个实数根;
④?a∈R,g(x)的导函数g′(x)有两个零点;
其中所有正确结论的序号是______.

①对于[-c,c]内的任意实数m,n(m<n),
>0恒成立,由函数的图象可以看出,函数在[-1,1]内不是单调增函数,故命题不正确;
②若b=0,则函数g(x)是奇函数,此命题正确,b=0时,g(x)=af(x)是一个奇函数;
③若a≥1,b<0,则方程g(x)=0必有3个实数根,本题中没有具体限定b的范围,故无法判断g(x)=0有几个根;
④a=0时,g(x)=b,g′(x)=0,结论不成立.
综上②正确
故答案为②.
| g(n)-g(m) |
| n-m |
②若b=0,则函数g(x)是奇函数,此命题正确,b=0时,g(x)=af(x)是一个奇函数;
③若a≥1,b<0,则方程g(x)=0必有3个实数根,本题中没有具体限定b的范围,故无法判断g(x)=0有几个根;
④a=0时,g(x)=b,g′(x)=0,结论不成立.
综上②正确
故答案为②.

练习册系列答案
相关题目
 在
在 处连续,试确定a的值
处连续,试确定a的值 在
在 平面上沿曲线运动,速度大小不 变,其在
平面上沿曲线运动,速度大小不 变,其在 轴
轴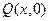 的运动速度
的运动速度 的图象大致为 ( )
的图象大致为 ( )




 的反函数是
的反函数是 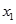 满足2x+
满足2x+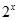 ="5,"
="5," 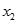 满足2x+2
满足2x+2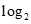 (x-1)="5,"
(x-1)="5," 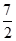
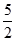
 的反函数是
的反函数是 则
则 。
。