题目内容
y=kx+3的图象先向左移动5个单位,再向上移动2个单位回到原来位置,则k=______.
设点P(a,b)是直线y=kx+3上的任意一点,则b=ak+3,
将点(a,b)先向左移动5个单位,得到点的坐标为(a-5,b),
再向上移动2个单位得到点的坐标为(a-5,b+2),此时点(a-5,b+2)在直线y=kx+3上,
所以b+2=k(a-5)+3,即b=ak+1-5k,
又b=ak+3,所以1-5k=3,所以k=-
.
故答案为:-
.
将点(a,b)先向左移动5个单位,得到点的坐标为(a-5,b),
再向上移动2个单位得到点的坐标为(a-5,b+2),此时点(a-5,b+2)在直线y=kx+3上,
所以b+2=k(a-5)+3,即b=ak+1-5k,
又b=ak+3,所以1-5k=3,所以k=-
| 2 |
| 5 |
故答案为:-
| 2 |
| 5 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
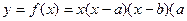 、
、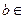 R)。
R)。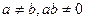 ,过两点(0,0)、(
,过两点(0,0)、(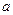 ,0)的中点作与
,0)的中点作与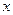 轴垂直的直线,与函数
轴垂直的直线,与函数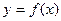 的图象交于点
的图象交于点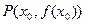 ,求证:函数
,求证:函数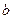 ,0)。
,0)。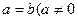 ),且当
),且当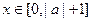 时
时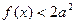 恒成立,求实数
恒成立,求实数 ,若函数
,若函数 的图象与函数
的图象与函数 的图象关于原点对称.(1)写出函数
的图象关于原点对称.(1)写出函数 的解析式;(2)求不等式
的解析式;(2)求不等式 的解集
的解集 ; (3)问是否存在
; (3)问是否存在 ,使不等式
,使不等式 的解集恰好是
的解集恰好是 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.







 的反函数是( )
的反函数是( )



 的反函数为_______.
的反函数为_______.