题目内容
在人寿保险业中,要重视某一年龄的投保人的死亡率,经过随机抽样统计,得到某市一个投保人能活到75岁的概率为0.60,试问:
(1)若有3个投保人, 求能活到75岁的投保人数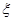 的分布列;
的分布列;
(2)3个投保人中至少有1人能活到75岁的概率.(结果精确到0.01)
(1)
(2)0.94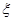
0 1 2 3 P 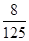
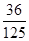
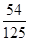
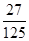
解析试题分析:(1) 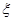 的可能取值为0,1,2,3, 1分
的可能取值为0,1,2,3, 1分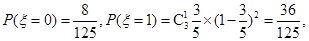
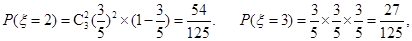 5分
5分
能活到75岁的投保人数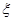 的分布列如下:
的分布列如下:
7分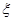
0 1 2 3 P 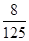
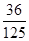
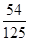
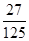
(2)3个投保人中至少有1人能活到75岁的概率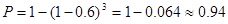 11分
11分
答: 3个投保人中至少有1人能活到75岁的概率是0.94 12分
考点:概率分布列
点评:求分布列的步骤:找到随机变量可以取得值,依次求出各随机变量值对应的概率,汇总得到分布列

练习册系列答案
相关题目
为了考察某种中药预防流感效果,抽样调查40人,得到如下数据:服用中药的有20人,其中患流感的有2人,而未服用中药的20人中,患流感的有8人。
(1)根据以上数据建立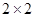 列联表;
列联表;
(2)能否在犯错误不超过0.05的前提下认为该药物有效?
参考
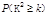 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
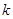 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
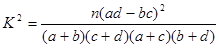 (
(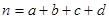 )
) 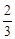 ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为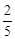 ,中奖可以获得3分;未中奖则不得分。每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品。
,中奖可以获得3分;未中奖则不得分。每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品。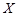 ,求
,求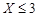 的概率;
的概率;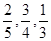 ,且假设各自能否被选中是无关的.
,且假设各自能否被选中是无关的.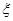 ,试求
,试求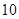 道题中,甲答对其中每道题的概率都是
道题中,甲答对其中每道题的概率都是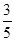 ,乙能答对其中的
,乙能答对其中的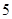 道题.规定每次考试都从备选的
道题.规定每次考试都从备选的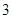 道题进行测试,答对一题加
道题进行测试,答对一题加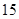 分才能入选.
分才能入选.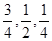 ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立.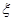 ,求
,求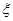 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求