题目内容
为了考察某种中药预防流感效果,抽样调查40人,得到如下数据:服用中药的有20人,其中患流感的有2人,而未服用中药的20人中,患流感的有8人。
(1)根据以上数据建立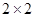 列联表;
列联表;
(2)能否在犯错误不超过0.05的前提下认为该药物有效?
参考
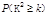 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
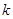 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
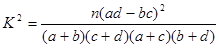 (
(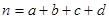 )
)
(1)
(1)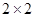 列联表
列联表
(2)在犯错误不超过0.05的前提下认为该药物有效 患流感 未患流感 总计 服用中药 2 18 20 未服用中药 8 12 20 总计 10 30 40
解析试题分析:解:(1)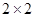 列联表
列联表
………6分 患流感 未患流感 总计 服用中药 2 18 20 未服用中药 8 12 20 总计 10 30 40
(2)根据列联表,计算: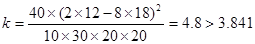
所以在犯错误不超过0.05的前提下认为该药物有效 12分
考点:独立性检验
点评:主要是考查了独立性检验的思想的运用,属于基础题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某市直小学为了加强管理,对全校教职工实行新的临时事假制度:“每位教职工每月在正常的工作时间,临时有事,可请假至多三次,每次至多一小时”.现对该制度实施以来50名教职工请假的次数进行调查统计,结果如下表所示:
| 请假次数 |  | 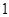 | 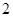 | 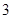 |
| 人数 | 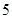 | 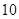 | 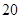 | 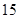 |
(1)从该小学任选两名教职工,用
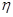 表示这两人请假次数之和,记“函数
表示这两人请假次数之和,记“函数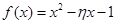 在区间
在区间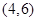 上有且只有一个零点”为事件
上有且只有一个零点”为事件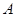 ,求事件
,求事件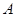 发生的概率
发生的概率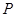 ;
;(2)从该小学任选两名职工,用
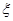 表示这两人请假次数之差的绝对值,求随机变量
表示这两人请假次数之差的绝对值,求随机变量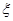 的分布列及数学期望
的分布列及数学期望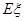 .
. 某工厂有甲、乙两个生产小组,每个小组各有四名工人,某天该厂每位工人的生产情况如下表.
| | 员工号 | 1 | 2 | 3 | 4 |
| 甲组 | 件数 | 9 | 11 | 1l | 9 |
| | 员工号 | 1 | 2 | 3 | 4 |
| 乙组 | 件数 | 9 | 8 | 10 | 9 |
(2)求乙组员工生产件数的平均数和方差;
(3)分别从甲、乙两组中随机选取一名员工的生产件数,求这两名员工的生产总件数为19的概率.
(注:方差
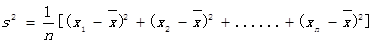 ,其中
,其中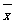 为x1,x2, ,xn的平均数)
为x1,x2, ,xn的平均数) 山东省某示范性高中为了推进新课程改革,满足不同层次学生的需求,决定从高一年级开始,在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座,每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座,也可以放弃任何一门科目的辅导讲座.(规定:各科达到预先设定的人数时称为满座,否则称为不满座)统计数据表明,各学科讲座各天的满座概率如下表:
| | 信息技术 | 生物 | 化学 | 物理 | 数学 |
| 周一 | 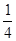 | 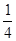 | 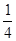 | 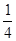 |  |
| 周三 |  |  |  |  | 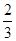 |
| 周五 |  |  |  |  | 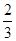 |
(Ⅱ)设周三各辅导讲座满座的科目数为
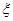 ,求随即变量
,求随即变量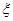 的分布列和数学期望.
的分布列和数学期望. 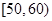 ,
, ,
,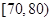 ,
,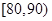 ,
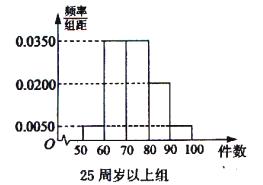
,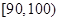 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.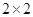 的列联表,并判断是否有
的列联表,并判断是否有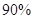 的把握认为“生产能手与工人所在的年龄组有关”?
的把握认为“生产能手与工人所在的年龄组有关”?

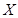 位,若连续抽取到两位愿意购买本地家禽的市民,或
位,若连续抽取到两位愿意购买本地家禽的市民,或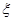 的分布列;
的分布列;  是从区间[0,3] 任 取 的一个数,
是从区间[0,3] 任 取 的一个数,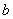 是从区间[0,2]任取的一个数,求上述方程有实根的概率.
是从区间[0,2]任取的一个数,求上述方程有实根的概率.