题目内容
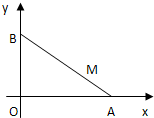
如图,线段AB的两个端点A、B分别分别在x轴、y轴上滑动,|AB|=5,点M是AB上一点,且|AM|=2,点M随线段AB的运动而变化.
(1)求点M的轨迹方程;
(2)设F1为点M的轨迹的左焦点,F2为右焦点,过F1的直线交M的轨迹于P,Q两点,求S△PQF2的最大值,并求此时直线PQ的方程.
(1)求点M的轨迹方程;
(2)设F1为点M的轨迹的左焦点,F2为右焦点,过F1的直线交M的轨迹于P,Q两点,求S△PQF2的最大值,并求此时直线PQ的方程.

(1)由题可知AM=
AB,且可设A(x0,0),M(x,y),B(0,y0),
则可得x0=
x,y0=
y,
又|AB|=5,即x02+y02=25,∴
+
=1,这就是点M的轨迹方程.
(2)由(1)知F1为(-
,0),F2为(
,0),
由题设PQ为x=my-
,
直线方程代入椭圆方程,可得(4m2+9)y2-8
my-16=0,
设P(x1,y1),Q(x2,y2),
则△>0恒成立,y1+y2=
且y1y2=
,
∴S△PQF2=
|F1F2|(|y1|+|y2|)=
|y1-y2|=24
•
令t=
(t≥1),则S△PQF1=24
•
≤6,
当且仅当t=
,即m=±
时取“=”
∴S△PQF2的最大值为6,
此时PQ的方程为2x+y-2
=0或2x-y-2
=0.
| 2 |
| 5 |
则可得x0=
| 5 |
| 3 |
| 5 |
| 2 |
又|AB|=5,即x02+y02=25,∴
| x2 |
| 9 |
| y2 |
| 4 |
(2)由(1)知F1为(-
| 5 |
| 5 |
由题设PQ为x=my-
| 5 |
直线方程代入椭圆方程,可得(4m2+9)y2-8
| 5 |
设P(x1,y1),Q(x2,y2),
则△>0恒成立,y1+y2=
8
| ||
| 4m2+9 |
| -16 |
| 4m2+9 |
∴S△PQF2=
| 1 |
| 2 |
| 5 |
| 5 |
| ||
| 4m2+9 |
令t=
| m2+1 |
| 5 |
| 1 | ||
4t+
|
当且仅当t=
| ||
| 2 |
| 1 |
| 2 |
∴S△PQF2的最大值为6,
此时PQ的方程为2x+y-2
| 5 |
| 5 |

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目