题目内容
【题目】陆良县2017届和2018届都取得了辉煌的成绩，两年均有人考入清华大学或北京大学，600分以上的考生进一步创历史新高.对此北辰中学某学习兴趣小组对2019届20名学生的数学成绩进行了调查，所得分数分组为
，
，，
，
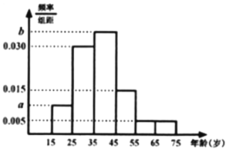
，据此制作的频率分布直方图如图所示.
（1）求出直方图中的
值；
（2）利用直方图估计2019届20名学生分数的众数和中位数（同一组中的数据用该组区间的中点值作代表）；
（3）若从分数在的学生中，随机的抽取2名学生进行辅导，求抽到的学生来自同一组的概率.
【答案】（1）
（2）中位数为126.7；众数为：125（3）
【解析】
（1）利用频率分布直方图中，小矩形的面积之和等于
可求
，
（2）频率分布直方图中，众数是小矩形面积最大的底边中点的横坐标；设中位数为
，结合图形可得
，解方程即可.
（3）在
的2名学生为
，在
的4名学生为
，列举出任选2人所有的基本事件，根据古典概型的概率计算公式即可求解.
解：（1）由频率分布直方图得：
∴
（2）由频率分布直方图得：2019届这20名学生分数的众数为：125；
设2019届这20名学生分数的中位数为，则满足：
∴
∴2019届这20名学生分数的中位数为126.7
（3）设事件
为从分数在
的学生中，随机的抽取2名学生进行辅导，抽到的这两名学生来自同一组.
则由题意得：假设的6名学生中，在的2名学生为，在的4名学生为；则任选2人的可能搭配情况为：
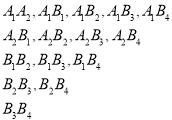
所以
.
【题目】某企业有甲、乙两套设备生产同一种产品，为了检测两套设备的生产质量情况，随机从两套设备生产的大量产品中各抽取了50件产品作为样本，检测一项质量指标值，若该项质量指标值落在
内，则为合格品，否则为不合格品. 表1是甲套设备的样本的频数分布表，图1是乙套设备的样本的频率分布直方图.
表1：甲套设备的样本的频数分布表
质量指标值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
频数 | 1 | 4 | 19 | 20 | 5 | 1 |
图1：乙套设备的样本的频率分布直方图
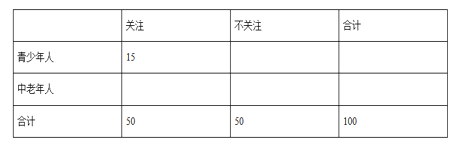
（1）填写下面列联表，并根据列联表判断是否有90%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关；
甲套设备 | 乙套设备 | 合计 | |||||||||||||
合格品 | |||||||||||||||
不合格品 | |||||||||||||||
合计 | ，求 |
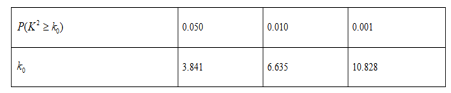
P(K2≥k0) | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
.
