题目内容
双曲线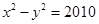
的左、右顶点分别为
、
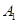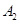，P为其右支上的一点，且
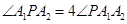，则
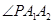等于（ ）
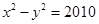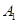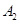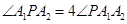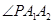的左、右顶点分别为、，P为其右支上的一点，且，则等于（ ）| A．无法确定 | B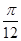． | C． | D． |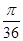
B
解：设a2=2010，
A1（-a，0），A2（a，0），P（x，y），
kPA1=tan∠PA1A2=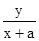
，①
kPA2=-tan∠PA2A1=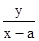
，②
由x2-y2=a2得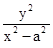
=1，
①×②，得-tan∠PA1A2tan∠PA2A1=1，
∴tan∠PA1A2tan（5∠PA1A2）=1
即tan（5∠PA1A2）=tan（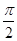
-∠PA1A2）
∴5∠PA1A2=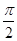-∠PA1A2
∴∠PA1A2=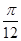
故选B．
A1（-a，0），A2（a，0），P（x，y），
kPA1=tan∠PA1A2=
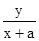，①kPA2=-tan∠PA2A1=
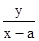，②由x2-y2=a2得
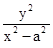=1，①×②，得-tan∠PA1A2tan∠PA2A1=1，
∴tan∠PA1A2tan（5∠PA1A2）=1
即tan（5∠PA1A2）=tan（
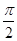-∠PA1A2）∴5∠PA1A2=
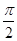-∠PA1A2∴∠PA1A2=
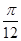
故选B．
练习册系列答案
寒假学与练系列答案
相关题目
的左准线上,过点P且方向为
=(-2,5)的光线经直线y=2反射后通过双曲线的左焦点,则这个双曲线的离心率为 
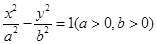的左、右焦点，P为双曲线左支上任一点，若
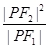的最小值为8a，则双曲线的离心率e的取值范围是（ ）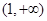
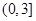
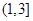
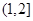
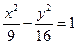的右焦点F作倾斜角为的直线交双曲线于A、B两点，求线段AB的中点C到焦点F的距离
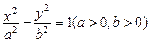的左、右焦点分别为
、
，
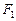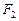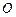为坐标原点，点
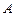在双曲线的右支上，点
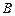在双曲线左准线上，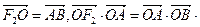
；
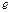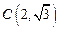，求双曲线的方程；
、
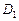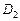分别是双曲线的虚轴端点（
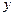轴正半轴上），过
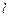交双曲线于点
、
，
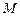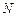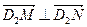，求直线
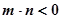是方程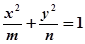
表示双曲线实轴在
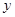轴的 （ ）
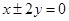，焦距为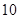
，这双曲线的方程为 .
直角坐标系
中，双曲线
的渐近线方程为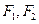 
，双曲线右支上一点P使得
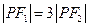，则双曲线的离心率范围是