题目内容
【题目】设![]() 是20个两两不同的正整数,且集合
是20个两两不同的正整数,且集合![]() 中有201个不同的元素.求集合
中有201个不同的元素.求集合![]() 中不同元素个数的最小可能值.
中不同元素个数的最小可能值.
【答案】100
【解析】
所给集合的元素个数的最小值为100.
例子:令![]() ,
,
![]() .
.
则![]() 中共有
中共有![]() 个不同的元素.
个不同的元素.
而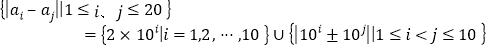
共有![]() 个不同的元素.
个不同的元素.
下面证明:所给集合的不同元素的个数不小于100.
用反证法证明.
若存在一个使所给集合的元素个数小于100的集合![]() .计算
.计算![]() 的“好子集”
的“好子集”![]() 的个数,这里,
的个数,这里,![]() ,且
,且![]() .
.
对![]() 中满足
中满足![]() 的数对
的数对![]() (共190对),考虑它们的差
(共190对),考虑它们的差![]() ,由假设知至多有99个不同的差,故必有至少91个数对
,由假设知至多有99个不同的差,故必有至少91个数对![]() ,使得存在
,使得存在![]() ,满足
,满足![]() ,
,![]() ,且
,且![]() .对这样的91个数对
.对这样的91个数对![]() ,它与其对应的
,它与其对应的![]() 、
、![]() 形成
形成![]() 的一个四元集
的一个四元集![]() ,可以得到
,可以得到![]() 的一个好子集
的一个好子集![]() ,且至多两个数对
,且至多两个数对![]() 形成相同的子集
形成相同的子集![]() (只能是
(只能是![]() 或
或![]() ).故S的好子集至少有46个.
).故S的好子集至少有46个.
另一方面,![]() 的好子集
的好子集![]() 的个数等于
的个数等于![]() ,这里,
,这里,![]() 为
为![]() 中满足
中满足![]() ,
,![]() 的数对
的数对![]() 的个数.
的个数.
注意到,对每个![]() ,
,![]() 中的每个元素
中的每个元素![]() 至多出现在上面的一个数对
至多出现在上面的一个数对![]() 中(事实上,当
中(事实上,当![]() 时,
时,![]() 出现在数对
出现在数对![]() 中,其余情况出现在
中,其余情况出现在![]() 中),于是,
中),于是,![]() .从而,在
.从而,在![]() 时,
时,![]() .故
.故![]() .
.
由于集合![]() 中有201个不同的元素,故使得
中有201个不同的元素,故使得![]() 的正整数
的正整数![]() 有201个.设
有201个.设![]() 为这样的
为这样的![]() 组成的集合,利用
组成的集合,利用![]() 中有
中有![]() 对
对![]() 满足
满足![]() ,有20对
,有20对![]() 满足
满足![]() ,故
,故![]() .
.
则![]() .
.
这与前面所得到的结论:![]() 的好子集至少有46个矛盾.
的好子集至少有46个矛盾.
因此,所给的集合中,至少有100个不同的元素.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目