题目内容
【题目】某“![]() ” 型水渠南北向宽为
” 型水渠南北向宽为![]() ,东西向宽为
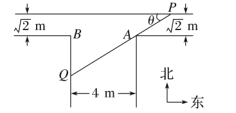
,东西向宽为![]() ,其俯视图如图所示.假设水渠内的水面始终保持水平位置.
,其俯视图如图所示.假设水渠内的水面始终保持水平位置.
(1) 过点![]() 的一条直线与水渠的内壁交于
的一条直线与水渠的内壁交于![]() 两点,且与水渠的一边的夹角为
两点,且与水渠的一边的夹角为![]() (
(![]() 为锐角),将线段
为锐角),将线段![]() 的长度
的长度![]() 表示为
表示为![]() 的函数;
的函数;
(2) 若从南面漂来一根长度为![]() 的笔直的竹竿(粗细不计),竹竿始终浮于水平面内,且不发生形变,问:这根竹竿能否从拐角处一直漂向东西向的水渠(不会卡住)?试说明理由.
的笔直的竹竿(粗细不计),竹竿始终浮于水平面内,且不发生形变,问:这根竹竿能否从拐角处一直漂向东西向的水渠(不会卡住)?试说明理由.
【答案】(1)![]() (2)能
(2)能
【解析】分析:(1)求出PA,QA,即可将线段PQ的长度l表示为![]() 的函数;
的函数;
(2)求导数,确定函数的单调性,即可得出结论.
解析:解(1)由题意,![]() ,
,![]() ,
,
所以![]()
(2)设![]() ,
,![]()
由![]() ,令
,令![]() ,得
,得![]() .
.
且当![]() ,
,![]() ;当
;当![]() ,
,![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以当![]() 时,
时,![]() 取得极小值,即为最小值.
取得极小值,即为最小值.
当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() 的最小值为
的最小值为![]() ,
,
即这根竹竿能通过拐角处的长度的最大值为![]() .
.
因为![]() ,所以这根竹竿能从拐角处一直漂向东西向的水渠.
,所以这根竹竿能从拐角处一直漂向东西向的水渠.
答:竹竿能从拐角处一直漂向东西向的水渠.

 考前必练系列答案
考前必练系列答案【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.某机构组织了一场诗词知识竞赛,将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,从中随机抽取100名选手进行调查,如图是根据调查结果绘制的选手等级与人数的条形图.
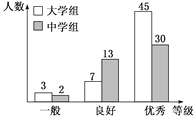
(1)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的2×2列联表,并据此判断能否在犯错误的概率不超过0.05的前提下认为选手成绩优秀与文化程度有关?
优秀 | 合格 | 总计 | |
大学组 | |||
中学组 | |||
总计 |
(2)若参赛选手共6万名,用频率估计概率,试估计其中优秀等级的选手人数;
(3)在优秀等级的选手中选取6名,在良好等级的选手中选取6名,都依次编号为1,2,3,4,5,6,在选出的6名优秀等级的选手中任取一名,记其编号为a,在选出的6名良好等级的选手中任取一名,记其编号为b,求使得方程组![]() 有唯一一组实数解(x,y)的概率.
有唯一一组实数解(x,y)的概率.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
P(K2≥k0) | 0.10 | 0.05 | 0.01 |
k0 | 2.706 | 3.841 | 6.635 |