题目内容
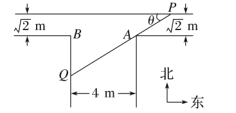
【题目】莱市在市内主于道北京路一侧修建圆形休闲广场.如图，圆形广场的圆心为
，半径为
，并与北京路一边所在直线
相切于点
.点
为上半圆弧上一点，过点作的垂线，垂足为点
.市园林局计划在
内进行绿化，设的面积为
（单位：
），
（单位：弧度）.
（1）将表示为
的函数；
（2）当绿化面积最大时，试确定点的位置，并求最大面积.
【答案】（1）
（2）点
到北京路一边
的距离为
；最大值
【解析】
（1）利用三角函数的定义求出
，
的长，利用三角形的面积公式求出
的面积
（2）对
求导，令导函数为0求出根，判断根左右两边导函数的符号，求出的最大值．
解：（1）如图，
，
则
.
（2）
.令
，
得
或
（舍去），
此时
当
变化时，
，的变化情况如下表：
|
|
|
|
|
|
|
|
|
| 极大值 |
|
所以，当时，取得最大值
，此时
，即点到北京路一边的距离为.
练习册系列答案
相关题目
【题目】2018年2月9-25日，第23届冬奥会在韩国平昌举行.4年后，第24届冬奥会将在中国北京和张家口举行.为了宣传冬奥会，某大学在平昌冬奥会开幕后的第二天，从全校学生中随机抽取了120名学生，对是否收看平昌冬奥会开幕式情况进行了问卷调查，统计数据如下：
收看 | 没收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
(Ⅰ)根据上表说明，能否有
的把握认为，收看开幕式与性别有关？
(Ⅱ)现从参与问卷调查且收看了开幕式的学生中，采用按性别分层抽样的方法选取8人，参加2022年北京冬奥会志愿者宣传活动.
(ⅰ)问男、女学生各选取多少人？
(ⅱ)若从这8人中随机选取2人到校广播站开展冬奥会及冰雪项目宣传介绍，求恰好选到一名男生一名女生的概率P.
附：
，其中
.
|
|
|
|
|
|
|
|
|
|
|
|
