题目内容
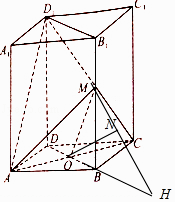
【题目】如图,长方体ABCD﹣A1B1C1D1中,点M在棱BB1上,两条直线MA,MC与平面ABCD所成角均为θ,AC与BD交于点O. 
(1)求证:AC⊥OM;
(2)当M为BB1的中点,且θ= ![]() 时,求二面角A﹣D1M﹣B1的余弦值.
时,求二面角A﹣D1M﹣B1的余弦值.
【答案】
(1)证明:∵MB⊥面ABCD,直线MA,MC与平面ABCD所成角均为θ,∴∠MAB=∠MCB=θ.
故△MBA≌MBC,BA=BC.
∴四边形ABCD为正方形,AC⊥DB,又AC⊥MB,DB∩MB=B
∴AC⊥面BDM,即AC⊥OM
(2)解:θ= ![]() 时,则有AB=BC=MB,延长D1M,DB交于点点H,
时,则有AB=BC=MB,延长D1M,DB交于点点H,
过点O作ON⊥D1H于点N,连接AN,则∠ANO为二面角A﹣D1M﹣B的平面角.
设AB=1,由△D1DH∽△ONH易得ON= ![]() ,AO=
,AO= ![]() ,
,
tan∠ANO= ![]() ,∴∠ANO=30°
,∴∠ANO=30°
二面角A﹣D1M﹣B1的余弦值为 ![]() .
.
【解析】(Ⅰ)由 MC与平面ABCD所成角均为θ,得∠MAB=∠MCB=θ.BA=BC.四边形ABCD为正方形,即可得AC⊥面BDM,即AC⊥OM.(Ⅱ) θ= ![]() 时,则有AB=BC=MB,延长D1M,DB交于点点H,过点O作ON⊥D1H于点N,连接AN,则∠ANO为二面角A﹣D1M﹣B的平面角,利用平面几何知识即可求解.
时,则有AB=BC=MB,延长D1M,DB交于点点H,过点O作ON⊥D1H于点N,连接AN,则∠ANO为二面角A﹣D1M﹣B的平面角,利用平面几何知识即可求解.
【考点精析】解答此题的关键在于理解直线与平面垂直的性质的相关知识,掌握垂直于同一个平面的两条直线平行.

练习册系列答案
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目


