题目内容
对实数a和b,定义运算“?”:a?b=
设函数f(x)=(x2-1)?(x-x2),x∈R.若函数y=f(x)-c恰有两个不同的零点,则实数c的取值范围是( )
设函数f(x)=(x2-1)?(x-x2),x∈R.若函数y=f(x)-c恰有两个不同的零点,则实数c的取值范围是( )A．(-∞,-1)∪(- ,0) | B．{-1,-} |
| C．(-1,-) | D．(-∞,-1)∪[-,0) |
A
由x2-1≤x-x2得-
≤x≤1,
∴f(x)=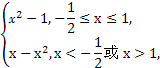
函数f(x)的图象如图所示,
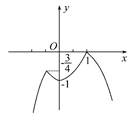
由图象知,当c<-1或-<c<0时,
函数y=f(x)-c恰有两个不同的零点.
≤x≤1,∴f(x)=
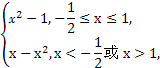
函数f(x)的图象如图所示,
由图象知,当c<-1或-
<c<0时,函数y=f(x)-c恰有两个不同的零点.
练习册系列答案
阅读快车系列答案
相关题目
)内各有一个零点,求实数a的范围.
若函数f(x)在[0,2]上的最大值比最小值大
,则a的值为 .
,可继续行驶距离=
;
.
的定义域为R，且定义如下：
（其中
是非空实数集）．若非空实数集
满足
，则函数
的值域为 ．
(x≠-
)满足f(f(x))=x,则常数c等于( )