题目内容
已知a>0,a≠1,函数f(x)=
若函数f(x)在[0,2]上的最大值比最小值大
,则a的值为 .
若函数f(x)在[0,2]上的最大值比最小值大,则a的值为 .
或
若a>1,则函数f(x)在[0,1]递增,[1,2]递减,
∴f(x)max=f(1)=a,
f(x)min=f(0)=1或f(x)min=f(2)=a-2,
∴
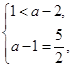或
故a=.
若0<a<1,
则f(x)在[0,1]递减,(1,2]递减,
∴f(x)max=f(0)=1,f(x)min=f(2)=a-2,
∴1-(a-2)=,得a=,
综上a=或a=.
∴f(x)max=f(1)=a,
f(x)min=f(0)=1或f(x)min=f(2)=a-2,
∴
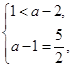或故a=
.若0<a<1,
则f(x)在[0,1]递减,(1,2]递减,
∴f(x)max=f(0)=1,f(x)min=f(2)=a-2,
∴1-(a-2)=
,得a=,综上a=
或a=.
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
立方米，且l≥2r.假设该容器的建造费用仅与其表面积有关，已知圆柱形部分每平方米建造费用为3千元，半球形部分每平方米建造费用为c(c>3)千元．设该容器的建造费用为y千元．
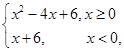则不等式f(x)>f(1)的解集是( )
在区间
内有一个零点，则实数
的取值可以是（ ）
设函数f(x)=(x2-1)?(x-x2),x∈R.若函数y=f(x)-c恰有两个不同的零点,则实数c的取值范围是( )
,0)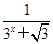
，求f(－12)＋f(－11)＋f(－10)＋…＋f(0)＋…＋f(11)＋f(12)＋f(13)的值．