Question

【题目】已知双曲线的中心在原点，焦点为，且离心率.

（1）求双曲线的方程；

（2）求以点为中点的弦所在的直线方程.

【答案】（1）；（2）.

【解析】

（1）根据焦点坐标求得,根据离心率及求得的值，进而求得双曲线的标准方程.（2）设出两点的坐标，利用点差法求得弦所在直线的斜率，再由点斜式求得弦所在的直线方程.

（1） 由题可得，，∴，,

所以双曲线方程 .

（2）设弦的两端点分别为，，

则由点差法有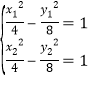： , 上下式相减有：

又因为为中点，所以，,

∴，所以由直线的点斜式可得,

即直线的方程为.

经检验满足题意.

【点睛】

本小题主要考查双曲线标准方程的求法，考查利用点差法求解有关弦的中点有关的问题，属于中档题.

【题型】解答题
【结束】
19

【题目】某投资公司计划投资，两种金融产品，根据市场调查与预测，产品的利润与投资金额的函数关系为，产品的利润与投资金额的函数关系为.（注：利润与投资金额单位：万元）

（1）该公司已有100万元资金，并全部投入，两种产品中，其中万元资金投入产品，试把，两种产品利润总和表示为的函数，并写出定义域；

（2）试问：怎样分配这100万元资金，才能使公司获得最大利润？其最大利润为多少万元？

Answer 1

【答案】（1）；（2）20，28.

【解析】

（1）设投入产品万元，则投入产品万元，根据题目所给两个产品利润的函数关系式，求得两种产品利润总和的表达式.（2）利用基本不等式求得利润的最大值，并利用基本不等式等号成立的条件求得资金的分配方法.

（1）其中万元资金投入产品，则剩余的（万元）资金投入产品，

利润总和为： ，

（2）因为，

所以由基本不等式得：,

当且仅当时，即：时获得最大利润28万.

此时投入A产品20万元，B产品80万元.