题目内容
1.若实数x,y满足:$\left\{{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{x≤4}\end{array}}\right.$,则$\frac{x}{y}$的取值范围是[$\frac{1}{3}$,+∞).分析 由约束条件作出可行域,数形结合求得$\frac{x}{y}$的取值范围.
解答 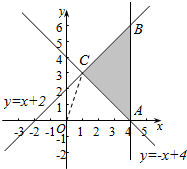 解:不等式组对应的可行域如图,
解:不等式组对应的可行域如图,
得A(4,0),C(1,3).利用斜率公式得结合图形可知,$\frac{y}{x}$的取值范围[0,3]
所以$\frac{x}{y}$的取值范围是[$\frac{1}{3}$,+∞).
故答案为:[$\frac{1}{3}$,+∞).
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知双曲线的渐近线方程为y=±$\frac{1}{2}$x,且经过点(4,1),则双曲线的标准方程为( )
| A. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{12}$=1 | B. | $\frac{{y}^{2}}{3}$-$\frac{{x}^{2}}{12}$=1 | C. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{3}$=1 | D. | $\frac{{y}^{2}}{12}$-$\frac{{x}^{2}}{3}$=1 |
10.已知函数f(x+1)的定义域为(-2,-1),则函数f(2x+1)的定义域为( )
| A. | (-5,-3) | B. | (-2,-$\frac{3}{2}$ ) | C. | (-$\frac{3}{2}$,-1)? | D. | (-1,-$\frac{1}{2}$) |
11.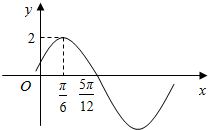 函数f(x)=Asin(ωx+φ)(其中A>0,$|\begin{array}{l}{φ}\end{array}|<\frac{π}{2}$)的图象如图所示,为了得到g(x)=2sin2x的图象,则只需将f(x)的图象( )
函数f(x)=Asin(ωx+φ)(其中A>0,$|\begin{array}{l}{φ}\end{array}|<\frac{π}{2}$)的图象如图所示,为了得到g(x)=2sin2x的图象,则只需将f(x)的图象( )
 函数f(x)=Asin(ωx+φ)(其中A>0,$|\begin{array}{l}{φ}\end{array}|<\frac{π}{2}$)的图象如图所示,为了得到g(x)=2sin2x的图象,则只需将f(x)的图象( )
函数f(x)=Asin(ωx+φ)(其中A>0,$|\begin{array}{l}{φ}\end{array}|<\frac{π}{2}$)的图象如图所示,为了得到g(x)=2sin2x的图象,则只需将f(x)的图象( )| A. | 向右平移$\frac{π}{6}$个长度单位 | B. | 向右平移$\frac{π}{12}$个长度单位 | ||
| C. | 向左平移$\frac{π}{6}$个长度单位 | D. | 向左平移$\frac{π}{12}$个长度单位 |
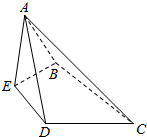 等边△ABC中,D,E分别是AC,AB的中点,沿DE将△ADE折起,使平面ADE⊥平面BCDE(如图所示).
等边△ABC中,D,E分别是AC,AB的中点,沿DE将△ADE折起,使平面ADE⊥平面BCDE(如图所示).