题目内容
已知函数 .
.
(Ⅰ)讨论函数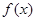 的单调性;
的单调性;
(Ⅱ)若对任意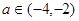 及
及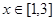 时,恒有
时,恒有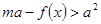 成立,求实数
成立,求实数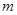 的取值范围.
的取值范围.
 .
.(Ⅰ)讨论函数
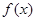 的单调性;
的单调性;(Ⅱ)若对任意
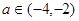 及
及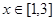 时,恒有
时,恒有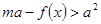 成立,求实数
成立,求实数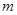 的取值范围.
的取值范围.(1)当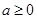 时,
时,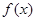 在
在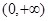 上是增函数;当
上是增函数;当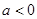 时,
时,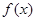 在
在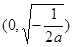 上是增函数,
上是增函数,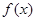 在
在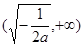 上是减函数.
上是减函数.
(2)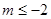
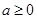 时,
时,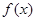 在
在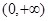 上是增函数;当
上是增函数;当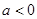 时,
时,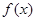 在
在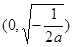 上是增函数,
上是增函数,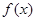 在
在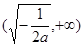 上是减函数.
上是减函数.(2)
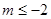
试题分析:解: (Ⅰ)
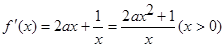 2分
2分①当
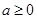 时,恒有
时,恒有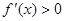 ,则
,则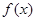 在
在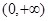 上是增函数; 4分
上是增函数; 4分②当
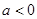 时,当
时,当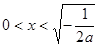 时,
时,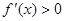 ,则
,则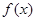 在
在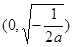 上是增函数;
上是增函数;当
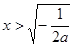 时,
时,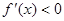 ,则
,则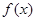 在
在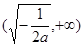 上是减函数 6分
上是减函数 6分综上,当
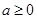 时,
时,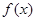 在
在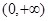 上是增函数;当
上是增函数;当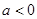 时,
时,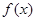 在
在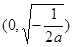 上是增函数,
上是增函数,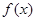 在
在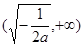 上是减函数. 7分
上是减函数. 7分(Ⅱ)由题意知对任意
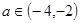 及
及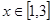 时,
时,恒有
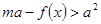 成立,等价于
成立,等价于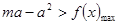
因为
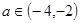 ,所以
,所以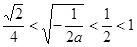
由(Ⅰ)知:当
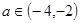 时,
时,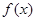 在
在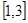 上是减函数
上是减函数所以
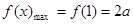 10分
10分所以
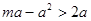 ,即
,即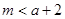
因为
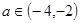 ,所以
,所以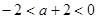
所以实数
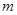 的取值范围为
的取值范围为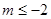 12分
12分点评:主要是考查了导数在研究函数中的运用,属于基础题。

练习册系列答案
相关题目
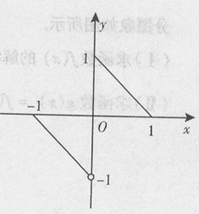
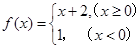 ,则
,则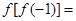 ( )
( )
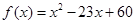 ,
,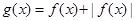 ,则
,则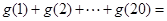 ( )
( )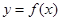 满足:
满足: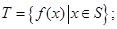 (ii)对任意
(ii)对任意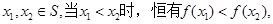
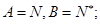
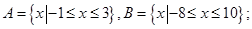
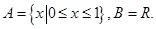
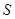 的最大允许值是多少?
的最大允许值是多少?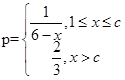 (其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.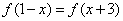 ,且
,且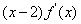 <0a="f" (
<0a="f" (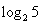 ),b="f" (
),b="f" (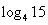 ),c="f" (
),c="f" (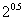 ),则a,b,c的大小关系为
),则a,b,c的大小关系为