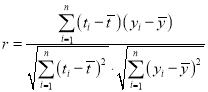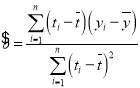题目内容
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)若![]() 是定义在
是定义在![]() 上的单调函数,求实数a的取值范围;
上的单调函数,求实数a的取值范围;
(2)当![]() 时,判断
时,判断![]() 与
与![]() 的图象在其公共点处是否存在公切线?若存在,求满足条件的a值的个数;若不存在,请说明理由.
的图象在其公共点处是否存在公切线?若存在,求满足条件的a值的个数;若不存在,请说明理由.
【答案】(1)![]() 或
或![]() ;(2)存在,理由见解析.
;(2)存在,理由见解析.
【解析】
(1)对函数求导,根据实数a的不同取值进行分类讨论,最后可以根据函数的单调区间求出实数a的取值范围;
(2))假设![]() ,
,![]() 的图象在其公共点
的图象在其公共点![]() 处存在公切线,对两个函数分别求导,根据点在函数图象上,和切线的斜率列出方程组,化简得到关于a的方程,构造新函数,根据新函数的零点情况进而可以判断出方程的根的情况,最后可以判断出是否存在公切线.
处存在公切线,对两个函数分别求导,根据点在函数图象上,和切线的斜率列出方程组,化简得到关于a的方程,构造新函数,根据新函数的零点情况进而可以判断出方程的根的情况,最后可以判断出是否存在公切线.
(1)![]() .
.
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上单调递减,满足题意;
上单调递减,满足题意;
当![]() 时,要使得
时,要使得![]() 在
在![]() 上单调,则恒有
上单调,则恒有![]() .
.
∴![]() ,解得:
,解得:![]() .
.
综上,![]() 或
或![]()
(2)假设![]() ,
,![]() 的图象在其公共点
的图象在其公共点![]() 处存在公切线,
处存在公切线,
则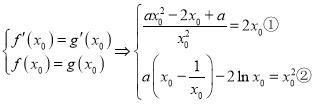
由①可得:![]()
∴![]() .
.
将![]() 代入②,则
代入②,则![]() ,即:
,即:![]() .
.
令![]() ,则
,则![]() ,故
,故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
又![]() ,且当
,且当![]() ,
,![]() ;当
;当![]() ,
,![]()
∴![]() 在
在![]() 有两个零点,即方程
有两个零点,即方程![]() 在
在![]() 有两个不同的解.
有两个不同的解.
所以,![]() 与
与![]() 的图象在其公共点处存在公切线,满足条件的a值有2个
的图象在其公共点处存在公切线,满足条件的a值有2个

练习册系列答案
相关题目
【题目】国家大力提倡科技创新,某工厂为提升甲产品的市场竞争力,对生产技术进行创新改造,使甲产品的生产节能降耗.以下表格提供了节能降耗后甲产品的生产产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨)的几组对照数据.
(吨)的几组对照数据.
|
|
|
|
|
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(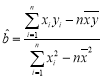 ,
,![]() )
)
(2)已知该厂技术改造前生产![]() 吨甲产品的生产能耗为
吨甲产品的生产能耗为![]() 吨,试根据(1)求出的线性回归方程,预测节能降耗后生产
吨,试根据(1)求出的线性回归方程,预测节能降耗后生产![]() 吨甲产品的生产能耗比技术改造前降低多少吨?
吨甲产品的生产能耗比技术改造前降低多少吨?