题目内容
【题目】正数数列![]() 、
、![]() 满足:
满足:![]() ≥
≥![]() ,且对一切k≥2,k
,且对一切k≥2,k![]() ,
,![]() 是
是![]() 与
与![]() 的等差中项,
的等差中项,![]() 是
是![]() 与
与![]() 的等比中项.
的等比中项.
(1)若![]() ,
,![]() ,求
,求![]() ,
,![]() 的值;
的值;
(2)求证:![]() 是等差数列的充要条件是
是等差数列的充要条件是![]() 为常数数列;
为常数数列;
(3)记![]() ,当n≥2(n
,当n≥2(n![]() )时,指出
)时,指出![]() 与
与![]() 的大小关系并说明理由.
的大小关系并说明理由.
【答案】(1)![]() ,
,![]() .(2)见解析(3)
.(2)见解析(3)![]()
【解析】
(1)由题意得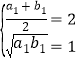 ,解方程组可得所求.(2)证明结论“当
,解方程组可得所求.(2)证明结论“当![]() 为常数数列时,
为常数数列时,![]() 是公差为零的等差数列”和“
是公差为零的等差数列”和“![]() 是等差数列时
是等差数列时![]() 为常数数列”同时成立即可.(3)由题意证得
为常数数列”同时成立即可.(3)由题意证得![]() ,进而得到
,进而得到![]() ,故得
,故得![]() ,然后通过数列求和可得结论成立.
,然后通过数列求和可得结论成立.
(1)由条件得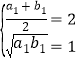 ,即
,即![]() ,
,
解得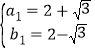 或
或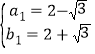 ,
,
又![]() ≥
≥![]() ,
,
所以![]() .
.
(2)(充分性):当![]() 为常数数列时,
为常数数列时,![]() 是公差为零的等差数列,即充分性成立.
是公差为零的等差数列,即充分性成立.
(必要性):因为![]()
![]()
![]()
![]()
![]()
![]() ,
,
又当![]() 为等差数列时,
为等差数列时,![]() 对任意
对任意![]() 恒成立.
恒成立.
所以![]() ,
,
因为![]() ,
,
所以![]() ,即
,即![]() ,
,
从而![]() 对
对![]() 恒成立,
恒成立,
所以![]() 为常数列.
为常数列.
综上可得![]() 是等差数列的充要条件是
是等差数列的充要条件是![]() 为常数数列.
为常数数列.
(3)因为任意![]() ,
,![]() ,
,
又![]() ,
,
所以![]() .
.
从而![]()
![]() ,
,
即![]() ,
,
则![]() ,
,
所以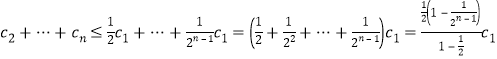
![]() .
.

练习册系列答案
相关题目