题目内容
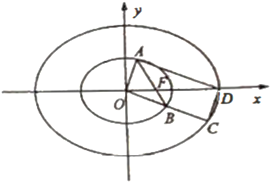
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 与
与![]() 的离心率相等.椭圆
的离心率相等.椭圆![]() 的右焦点为F,过点F的直线与椭圆
的右焦点为F,过点F的直线与椭圆![]() 交于A,B两点,射线
交于A,B两点,射线![]() 与椭圆
与椭圆![]() 交于点C,椭圆
交于点C,椭圆![]() 的右顶点为D.
的右顶点为D.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)若![]() ,求证:四边形
,求证:四边形![]() 是平行四边形.
是平行四边形.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)由题得![]() ,解方程即得
,解方程即得![]() 的值,即得椭圆
的值,即得椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 的方程为
的方程为![]() ,联立
,联立![]() ,得到韦达定理,再根据
,得到韦达定理,再根据![]()
![]()
![]() 求出
求出![]() 的值,即得直线
的值,即得直线![]() 的方程;
的方程;
(3)设![]() 先求出
先求出![]() 的坐标,得到
的坐标,得到![]() .所以
.所以![]() ,又
,又![]() ,所以
,所以![]() .即得四边形
.即得四边形![]() 是平行四边形.
是平行四边形.
(1)由题意知,椭圆![]() 的长轴长
的长轴长![]() ,短轴长
,短轴长![]() ,焦距
,焦距![]() ,
,
椭圆![]() 的长轴长
的长轴长![]() ,短轴长
,短轴长![]() ,焦距
,焦距![]() .
.
因为椭圆![]() 与
与![]() 的离心相等,所以
的离心相等,所以![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)因为椭圆![]() 右焦点为
右焦点为![]() ,且A,O,B三点不共线,
,且A,O,B三点不共线,
设直线![]() 的方程为
的方程为![]() ,联立
,联立![]() ,
,
消x得![]() .
.
设![]() ,
,![]() ,
,![]() ,
,
所以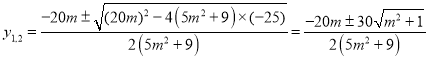 ,
,
即![]() .
.
因为![]()
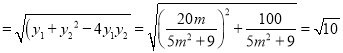 ,
,
化简得![]() ,所以
,所以![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
(3)因为![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以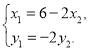
因为![]() 在椭圆
在椭圆![]() 上,
上,
所以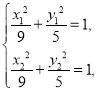 ,所以
,所以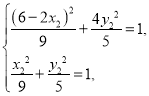 消
消![]() ,得
,得![]() .
.
代入![]() ,由对称性不妨设
,由对称性不妨设![]() ,所以
,所以![]() ,
,
从而得,![]() ,
,
即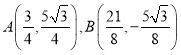 .
.
所以![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
联立![]() ,得
,得![]() .
.
由题知![]() ,所以
,所以![]() ,所以
,所以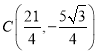 .
.
又![]() ,所以
,所以![]() .
.
又因为![]() 不共线,所以
不共线,所以![]() ,
,
又![]() ,且
,且![]() 不共线,所以
不共线,所以![]() .
.
所以四边形![]() 是平行四边形.
是平行四边形.

 阅读快车系列答案
阅读快车系列答案【题目】第七届世界军人运动会于2019年10月18日至27日(共10天)在武汉召开,人们通过手机、电视等方式关注运动会盛况.某调查网站从观看运动会的观众中随机选出200人,经统计这200人中通过传统的传媒方式电视端口观看的人数与通过新型的传媒方式![]() 端口观看的人数之比为
端口观看的人数之比为![]() .将这200人按年龄分组:第1组
.将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() .其中统计通过传统的传媒方式电视端口观看的观众得到的频率分布直方图如图所示.
.其中统计通过传统的传媒方式电视端口观看的观众得到的频率分布直方图如图所示.
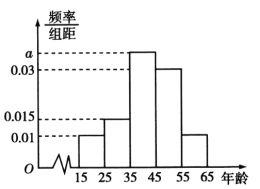
(1)求![]() 的值及通过传统的传媒方式电视端口观看的观众的平均年龄;
的值及通过传统的传媒方式电视端口观看的观众的平均年龄;
(2)把年龄在第1,2,3组的观众称为青少年组,年龄在第4,5组的观众称为中老年组,若选出的200人中通过新型的传媒方式![]() 端口观看的中老年人有12人,请完成下面
端口观看的中老年人有12人,请完成下面![]() 列联表,则能否在犯错误的概率不超过0.1的前提下认为观看军人运动会的方式与年龄有关?
列联表,则能否在犯错误的概率不超过0.1的前提下认为观看军人运动会的方式与年龄有关?
通过 | 通过电视端口观看军人运动会 | 合计 | |
青少年 | |||
中老年 | |||
合计 |
span>
附: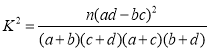 (其中
(其中![]() ).
).
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】为提倡节能减排,同时减轻居民负担,广州市积极推进“一户一表”工程![]() 非一户一表用户电费采用“合表电价”收费标准:
非一户一表用户电费采用“合表电价”收费标准:![]() 元
元![]() 度
度![]() “一户一表”用户电费采用阶梯电价收取,其11月到次年4月起执行非夏季标准如下:
“一户一表”用户电费采用阶梯电价收取,其11月到次年4月起执行非夏季标准如下:
第一档 | 第二档 | 第三档 | |
每户每月用电量 |
|
|
|
电价 |
|
|
|
例如:某用户11月用电410度,采用合表电价收费标准,应交电费![]() 元,若采用阶梯电价收费标准,应交电费
元,若采用阶梯电价收费标准,应交电费![]() 元.
元.
为调查阶梯电价是否能到“减轻居民负担”的效果,随机调查了该市100户的11月用电量,工作人员已经将90户的月用电量填在下面的频率分布表中,最后10户的月用电量![]() 单位:度
单位:度![]() 为:88、268、370、140、440、420、520、320、230、380.
为:88、268、370、140、440、420、520、320、230、380.

(1)在答题卡中完成频率分布表,并绘制频率分布直方图;

![]() 根据已有信息,试估计全市住户11月的平均用电量
根据已有信息,试估计全市住户11月的平均用电量![]() 同一组数据用该区间的中点值作代表
同一组数据用该区间的中点值作代表![]() ;
;
![]() 设某用户11月用电量为x度
设某用户11月用电量为x度![]() ,按照合表电价收费标准应交
,按照合表电价收费标准应交![]() 元,按照阶梯电价收费标准应交
元,按照阶梯电价收费标准应交![]() 元,请用x表示
元,请用x表示![]() 和
和![]() ,并求当
,并求当![]() 时,x的最大值,同时根据频率分布直方图估计“阶梯电价”能否给不低于
时,x的最大值,同时根据频率分布直方图估计“阶梯电价”能否给不低于![]() 的用户带来实惠?
的用户带来实惠?