题目内容
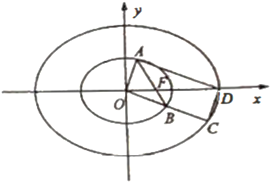
【题目】设D是圆O:x2+y2=16上的任意一点,m是过点D且与x轴垂直的直线,E是直线m与x轴的交点,点Q在直线m上,且满足2|EQ|![]() |ED|.当点D在圆O上运动时,记点Q的轨迹为曲线C.
|ED|.当点D在圆O上运动时,记点Q的轨迹为曲线C.
(1)求曲线C的方程.
(2)已知点P(2,3),过F(2,0)的直线l交曲线C于A,B两点,交直线x=8于点M.判定直线PA,PM,PB的斜率是否依次构成等差数列?并说明理由.
【答案】(1)![]() 1,(2)成等差数列
1,(2)成等差数列
【解析】
(1)由题意设Q(x,y),D(x0,y0),根据2|EQ|![]() |ED|Q在直线m上,则椭圆的方程即可得到;
|ED|Q在直线m上,则椭圆的方程即可得到;
(2)设出直线l的方程,和椭圆方程联立,利用根与系数的关系得到k1+k3,并求得k2的值,由k1+k3=2k2说明直线PA,PM,PB的斜率成等差数列.
解:(1)设Q(x,y),D(x0,y0),∵2|EQ|![]() |ED|,Q在直线m上,
|ED|,Q在直线m上,
∴x0=x,|y0|=|![]() y|.①
y|.①
∵点D在圆x2+y2=16上运动,
∴x02+y02=16,
将①式代入②式即得曲线C的方程为x2![]() y2=16,即
y2=16,即![]() 1,
1,
(2)直线PA,PM,PB的斜率成等差数列,证明如下:
由(1)知椭圆C:3x2+4y2=48,
直线l的方程为y=k(x﹣2),
代入椭圆方程并整理,得(3+4k2)x2﹣16k2x+16k2﹣48=0.
设A(x1,y1),B(x2,y2),直线PA,PM,PB的斜率分别为k1,k2,k3,
则有x1+x2![]() ,x1x2
,x1x2![]() ,
,
可知M的坐标为(8,6k).
∴k1+k3![]()
=2k﹣3![]() 2k﹣3
2k﹣3![]() 2k﹣1,
2k﹣1,
2k2=2![]() 2k﹣1.
2k﹣1.
∴k1+k3=2k2.
故直线PA,PM,PB的斜率成等差数列.

练习册系列答案
相关题目