题目内容
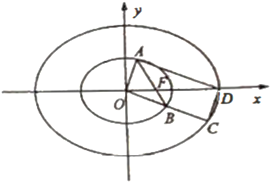
【题目】已知双曲线![]() 与圆
与圆![]() 在第一象限交点为
在第一象限交点为![]() ,曲线
,曲线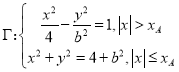 .
.
(1)若![]() ,求b;
,求b;
(2)若![]() ,
,![]() 与x轴交点是
与x轴交点是![]() ,P
,P![]() 是曲线
是曲线![]() 上一点,且在第一象限,并满足
上一点,且在第一象限,并满足![]() ,求∠
,求∠![]() ;
;
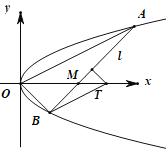
(3)过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于M、N两点,用b的代数式表示
于M、N两点,用b的代数式表示![]() ,并求出
,并求出![]() 的取值范围.
的取值范围.
【答案】(1)2;(2)![]() ;(3)
;(3)![]() ;
;![]() .
.
【解析】
(1)根据双曲线和圆的方程,将点![]() 的坐标代入,得到方程组,求得
的坐标代入,得到方程组,求得![]() 的值;
的值;
(2)方法一:结合双曲线的定义,得到![]() 的三边长,利用余弦定理求解;
的三边长,利用余弦定理求解;
方法二:根据![]() ,和双曲线的方程,联立方程组,求得
,和双曲线的方程,联立方程组,求得![]() 的坐标,进而利用向量的坐标运算和向量的夹角余弦值公式求解;
的坐标,进而利用向量的坐标运算和向量的夹角余弦值公式求解;
(3)根据直线![]() 的方程,判定是圆的切线,切点为
的方程,判定是圆的切线,切点为![]() ,并利用直线
,并利用直线![]() 的方程与圆的方程联立求得
的方程与圆的方程联立求得![]() 的坐标,注意到直线
的坐标,注意到直线![]() 与双曲线的斜率为负值的渐近线平行,利用数形结合思想,可得只有当
与双曲线的斜率为负值的渐近线平行,利用数形结合思想,可得只有当![]() 时,直线
时,直线![]() 才能与曲线
才能与曲线![]() 有两个交点,然后联立圆和双曲线的方程,求得
有两个交点,然后联立圆和双曲线的方程,求得![]() 的纵坐标关于
的纵坐标关于![]() 的函数表达式,进而解不等式求得
的函数表达式,进而解不等式求得![]() ,最后利用向量的数量积的运算得到
,最后利用向量的数量积的运算得到![]() 的取值范围.
的取值范围.
(1)若![]() ,因为点A为曲线
,因为点A为曲线![]() 与曲线
与曲线![]() 的交点,
的交点,
∵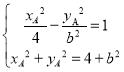 ,解得
,解得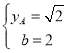 ,
,
∴![]() ;
;
(2)方法一:由题意易得![]() 为曲线的两焦点,因为
为曲线的两焦点,因为![]() ∴
∴![]() ,
,
又∵P在第一象限,由双曲线定义知:![]() ,
,
![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
在![]() 中由余弦定理可得:
中由余弦定理可得:
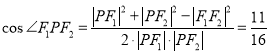 ;
;
方法二:∵![]() ,可得
,可得 ,解得
,解得![]() ,
,
![]()
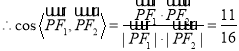 ;
;
(3)设直线![]() ,
,
可得原点O到直线![]() 的距离
的距离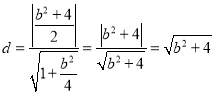 ,
,
所以直线![]() 是圆的切线,切点为M,
是圆的切线,切点为M,
所以![]() ,并设
,并设![]() ,与圆
,与圆![]() 联立可得
联立可得![]() ,
,
所以得![]() ,即
,即![]() ,
,
直线![]() 的斜率为
的斜率为![]() ,双曲线的渐近线方程为
,双曲线的渐近线方程为![]() ,
,
所以直线![]() 与双曲线的斜率为负值的渐近线平行,
与双曲线的斜率为负值的渐近线平行,
所以只有当![]() 时,直线
时,直线![]() 才能与曲线
才能与曲线![]() 有两个交点,
有两个交点,
由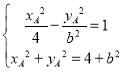 ,得
,得![]() ,
,
所以有![]() ,得
,得![]() ,
,
又因为:![]() ,
,
所以![]() .
.

练习册系列答案
相关题目