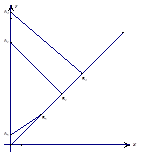
题目内容
定义数列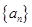 :
: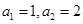 ,且对任意正整数
,且对任意正整数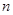 ,有
,有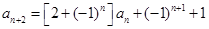 .
.
(1)求数列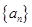 的通项公式与前
的通项公式与前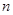 项和
项和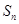 ;
;
(2)问是否存在正整数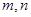 ,使得
,使得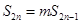 ?若存在,则求出所有的正整数对
?若存在,则求出所有的正整数对
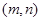 ;若不存在,则加以证明.
;若不存在,则加以证明.
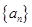 :
: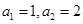 ,且对任意正整数
,且对任意正整数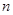 ,有
,有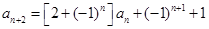 .
.(1)求数列
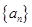 的通项公式与前
的通项公式与前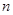 项和
项和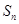 ;
;(2)问是否存在正整数
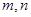 ,使得
,使得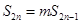 ?若存在,则求出所有的正整数对
?若存在,则求出所有的正整数对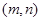 ;若不存在,则加以证明.
;若不存在,则加以证明.(1) ,
, ;
;
(2)见解析.
 ,
, ;
;(2)见解析.
考查了等差、等比数列的通项公式、求和公式,数列的分组求和等知识,考查了学生变形的能力,推理能力,探究问题的能力,分类讨论的数学思想、化归与转化的思想以及创新意识.
解:(1)对任意正整数k,
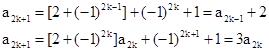 ,
,
. 1分
所以数列 是首项
是首项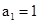 ,公差为2等差数列;数列
,公差为2等差数列;数列 是首项
是首项
 ,公比为3的等比数列. 2分
,公比为3的等比数列. 2分
对任意正整数k,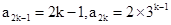 ,. 3分
,. 3分
所以数列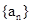 的通项公式
的通项公式 4分
4分
对任意正整数k,
 . 5分
. 5分
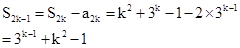 6分
6分
所以数列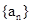 的前n项和为
的前n项和为
 . 7分
. 7分
(2) ,
,
从而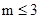 ,由
,由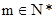 知m=1,2,3 8分
知m=1,2,3 8分
①当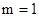 时,
时, 9分
9分
②当 时,
时, 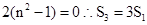 10分
10分
③当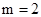 时,
时,
 13分
13分
综上可知,符合条件的正整数对(m,n)只有两对:(2,2,)与(3,1) 14分
解:(1)对任意正整数k,
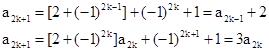 ,
,. 1分
所以数列
 是首项
是首项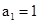 ,公差为2等差数列;数列
,公差为2等差数列;数列 是首项
是首项 ,公比为3的等比数列. 2分
,公比为3的等比数列. 2分对任意正整数k,
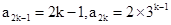 ,. 3分
,. 3分所以数列
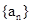 的通项公式
的通项公式 4分
4分对任意正整数k,
 . 5分
. 5分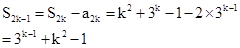 6分
6分所以数列
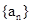 的前n项和为
的前n项和为 . 7分
. 7分(2)
 ,
,从而
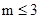 ,由
,由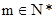 知m=1,2,3 8分
知m=1,2,3 8分①当
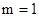 时,
时, 9分
9分②当
 时,
时, 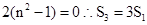 10分
10分 ③当
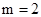 时,
时, 13分
13分 综上可知,符合条件的正整数对(m,n)只有两对:(2,2,)与(3,1) 14分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
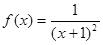 ,数列
,数列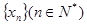 的项满足:
的项满足: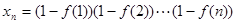 ,(1)试求
,(1)试求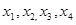
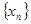 的通项,并利用数学归纳法证明.
的通项,并利用数学归纳法证明.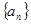 满足
满足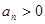 且对一切
且对一切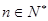 ,
,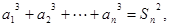
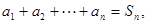
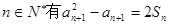
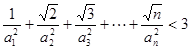
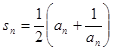 .
.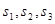 ;
;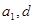 为实数,首项为
为实数,首项为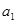 ,公差为
,公差为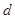 的等差数列
的等差数列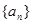 的前n项和为
的前n项和为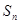 ,满足
,满足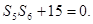
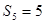 ,求
,求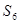 及
及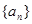 满足
满足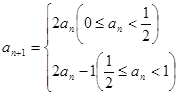 若
若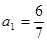 ,则
,则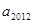 的值为:( )
的值为:( )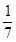
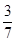
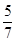
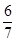
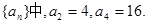
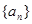 的通项公式;
的通项公式;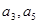 分别是等差数列
分别是等差数列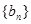 的第3项和第5项,求数列
的第3项和第5项,求数列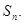
 (n=2,3,4,…). 在射线y=x(x≥0)上依次有点B1,B2,…,Bn,…,点B1的坐标为(3,3),且
(n=2,3,4,…). 在射线y=x(x≥0)上依次有点B1,B2,…,Bn,…,点B1的坐标为(3,3),且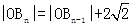 (n=2,3,4,…).
(n=2,3,4,…). ;
; 面积的最大值.
面积的最大值.