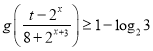Question

【题目】某辆汽车以千米小时的速度在高速公路上匀速行驶（考虑到高速公路行车安全要求时，每小时的油耗（所需要的汽油量）为升，其中为常数，且．

（1）若汽车以120千米小时的速度行驶时，每小时的油耗为11.5升，欲使每小时的油耗不超过9升，求的取值范围；

（2）求该汽车行驶100千米的油耗的最小值．

Answer 1

【答案】（1），；（2）当，该汽车行驶100千米的油耗的最小值为升；

当，该汽车行驶100千米的油耗的最小值为升．

【解析】

（1）将代入每小时的油耗，解方程可得，由题意可得，解不等式可得的范围；

（2）设该汽车行驶100千米油耗为升，由题意可得，换元令、化简整理可得的二次函数，讨论的范围和对称轴的关系，即可得到所求最小值．

解：（1）由题意可得当时，，

解得，由，

即，解得，

又，可得，

每小时的油耗不超过9升，的取值范围为，；

（2）设该汽车行驶100千米油耗为升，则

，

令，则，，

即有，

对称轴为，由，可得，，

①若即，

则当，即时，；

②若即，

则当，即时，．

答：当，该汽车行驶100千米的油耗的最小值为升；

当，该汽车行驶100千米的油耗的最小值为升．