题目内容
【题目】已知函数![]() (a为实常数).
(a为实常数).
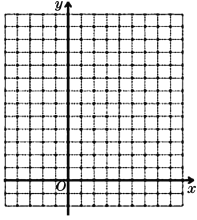
(1)若![]() ,作函数
,作函数![]() 的图象并写出单调减区间;
的图象并写出单调减区间;
(2)当![]() 时,设
时,设![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,求
,求![]() 的表达式;
的表达式;
(3)当![]() 时对于函数
时对于函数![]() 和函数
和函数![]() ,若对任意的
,若对任意的![]() ,总存在
,总存在![]() 使
使![]() 成立,求实数m的值.
成立,求实数m的值.
【答案】(1)图见解析,单调减区间:![]() ,
,![]() ;(2)
;(2)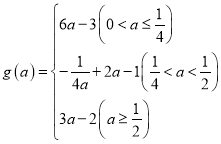 (3)-1
(3)-1
【解析】
(1)代入![]() 得
得![]() ,再分段求解析式即可.
,再分段求解析式即可.
(2)易得![]() 图象的对称轴是直线
图象的对称轴是直线![]() ,再分
,再分![]() 与区间
与区间![]() 的位置关系讨论
的位置关系讨论![]() 的最小值即可.
的最小值即可.
(3)根据题意可知![]() 的值域是
的值域是![]() 值域的子集,再列出区间端点满足的关系式求解即可.
值域的子集,再列出区间端点满足的关系式求解即可.
解:(1)当![]() 时,
时,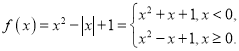
作图如下
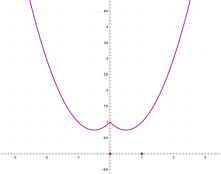
单调减区间:![]() ,
,![]() ;
;
(2)当![]() 时,
时,![]() .
.
![]() 图象的对称轴是直线
图象的对称轴是直线![]() .
.
当![]() ,即
,即![]() 时,
时,![]() 在区间
在区间![]() 上是增函数,
上是增函数,
![]() .
.
当![]() ,即
,即![]() 时,
时,![]() .
.
当![]() ,即
,即![]() 时,
时,![]() 在区间
在区间![]() 上是减函数,
上是减函数,
![]() .
.
综上可得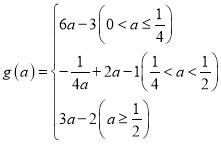 .
.
(3)![]() 的值域为
的值域为![]() ,
,![]() 在
在![]() 上的值域为
上的值域为![]() ,由题意可知
,由题意可知![]() 的值域是
的值域是![]() 值域的子集
值域的子集
所以![]() ,
,![]()

练习册系列答案
相关题目