Question

【题目】如图，△ABC的外接圆⊙O的半径为5，CE垂直于⊙O所在的平面，BD∥CE，CE＝4，BC＝6，且BD＝1，.

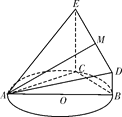
（1）求证：平面AEC⊥平面BCED；

（2）试问线段DE上是否存在点M，使得直线AM与平面ACE所成角的正弦值为？若存在，确定点M的位置；若不存在，请说明理由．

Answer 1

【答案】（1）答案详见解析；（2）存在，且．

【解析】

试题（1）要证明面面垂直，只需证明一个平面另一个平面的一条垂线，本题在中，求得，从而得为⊙O的直径，故，从而可证明面，进而证明平面AEC⊥平面BCED；（2）以方向为轴的正方向建立空间直角坐标系，用坐标表示相关点，利用表示向量的坐标，利用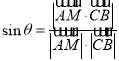列方程求的值，从而确定点的位置．

试题解析：（1）证明：∵平面．

∴，又因为，.

故AD＝，AB＝10＝直径长，（3分）

∴AC⊥BC.又因为EC⊥平面ABC，所以EC⊥BC.

∵AC∩EC＝C，∴BC⊥平面ACE，又BC平面BCED，

∴平面AEC⊥平面BCED.（6分）

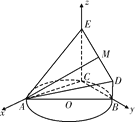
（2）法一：存在，如图，以C为原点，直线CA为x轴，直线CB为y轴，直线CE为z轴建立空间直角坐标系，则有点的坐标，A（8，0，0），B（0，6，0），D（0，6，1），E（0，0，4）．

则＝（－8，6，1），＝（0，－6，3），

设＝λ＝λ（0，－6，3）＝（0，－6λ，3λ），0<λ<1

故＝＋＝（－8, 6－6λ，1＋3λ）

由（1）易得平面ACE的法向量为＝（0，6，0），

设直线AM与平面ACE所成角为θ，

则sin θ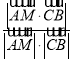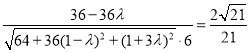＝＝，解得λ＝.（10分）

所以存在点M，且时，直线AM与平面ACE所成角的正弦值为． （12分）

法二：（几何法）

如图，作MN⊥CE交CE于N，连接AN，则MN⊥平面AEC，故直线AM与平面ACE所成的角为∠MAN，且MN⊥AN，NC⊥AC.

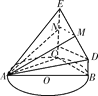
设MN＝2x，由直线AM与平面ACE所成角的正弦值为，得AM＝x，所以AN＝x.

另一方面，作DK∥MN∥BC，得EN＝x，NC＝4－x

而AC＝8，故Rt△ANC中，由AN2＝AC2＋NC2

得17x2＝64＋（4－x）2，∴x＝2，∴MN＝4，EM＝2

所以存在点，且时，直线与平面所成角的正弦值为. （12分）