Question

【题目】在平面直角坐标系xOy中，过点的圆的圆心C在x轴上，且与过原点倾斜角为30°的直线l相切.

(1)求圆C的标准方程；

(2)求直线被圆C截得的弦长；

(3)点P在直线m：上，过点P作⊙C的切线PM、PN，切点分别为M、N，求经过P、M、N、C四点的圆所过的定点坐标.

Answer 1

【答案】(1)；(2)；(3)或.

【解析】

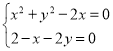（1）设⊙C的方程为，解方程组即得解；（2）利用直线和圆相交的弦长公式得解；（3）易知过P、M、C、N四点的圆以PC为直径，设，圆方程为，整理得，解方程组得解.

(1)设⊙C的方程为

又直线l的方程为：，即

由题意，解得：，，

∴⊙C的标准方程为

(2)圆心到直线的距离

故弦长

(3)易知过P、M、C、N四点的圆以PC为直径，

设，又C为，故所求圆的圆心为，半径为，

∴该圆方程为：

化一般方程得：

上述方程关于参数b重新整理得：，

令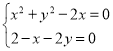，解得：或，

故所得圆过定点或.